|
Решение. Ответ для n домов: можно построить 2n – 1 заборов. В самом деле, если дом один, то можно построить только один забор, что соответствует формуле 2 · 1 – 1 = 1.
Дальше применим индукцию. Если для 1, 2,..., (n - 1) домов
формула 2n - 1 уже проверена, то рассмотрим n домов, вокруг которых построено максимально возможное количество заборов.
Какой-то забор огораживает все дома. Если этот внешний забор снести, то самыми внешними станут некоторые два забора. Внутри одного из них будет некоторое число k домов, а внутри другого — остальные n - k домов. Поскольку k < n, вокруг k домов может быть построено, самое большее,
2k - 1 заборов.
Аналогично, вокруг остальных n - k домов может быть построено, самое большее, 2(n - k) - 1 заборов. Значит, всего заборов не более
(2k - 1) + (2(n - k) - 1) + 1 = 2n - 1. |
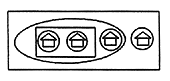 В посёлке 100 домов. Сколько заборов, не пересекающих друг друга, можно построить, чтобы каждый забор огораживал хотя бы один дом и никакие два забора не огораживали одну и ту же совокупность домов?
В посёлке 100 домов. Сколько заборов, не пересекающих друг друга, можно построить, чтобы каждый забор огораживал хотя бы один дом и никакие два забора не огораживали одну и ту же совокупность домов?