|
130.
| 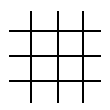 а) На рисунке 6 отрезков расположены так, что каждый пересекает три других отрезка. Расположите 8 отрезков, чтобы каждый пересекал три других отрезка. а) На рисунке 6 отрезков расположены так, что каждый пересекает три других отрезка. Расположите 8 отрезков, чтобы каждый пересекал три других отрезка.
б) Нарисуйте четыре горизонтальных и четыре вертикальных отрезка, чтобы каждый отрезок пересекал три отрезка другого направления. (То есть каждый вертикальный — три горизонтальных, а каждый горизонтальный — три вертикальных.)
|
Ответ |
|
Ответ. а) Поскольку 8 = 4 + 4, можно нарисовать четыре попарно пересекающихся отрезка и на некотором удалении от них — ещё четыре попарно пересекающихся друг с другом (но не с четырьмя предыдущими) отрезка:

Есть и другие способы, например:
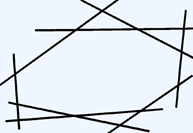
б)
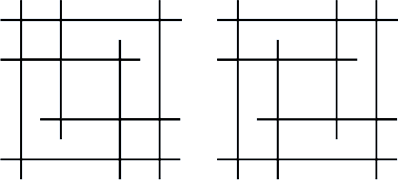
| | | |
|
131.
| Трём хирургам необходимо последовательно прооперировать в полевых условиях больного, страдающего заразным заболеванием. Сами хирурги тоже больны, причём все — разными болезнями. В распоряжении хирургов есть лишь две пары стерильных перчаток. Подскажите план операции, после которой ни хирурги, ни больной не заразятся друг от друга. (Помогать друг другу во время операций хирурги не должны. Оперировать одной рукой нельзя.)
|
Ответ |
|
Ответ. Первый хирург может надевает сразу две пары перчаток. Затем второй хирург наденет ту пару, которая была внешней во время первой операции. А третий хирург будет делать операцию опять в двух парах перчаток, причём внешняя останется внешней, а пара перчаток, бывшая во время первой операции внутренней, остаётся внутренней, но её выворачивают наизнанку.
| | | |
|
132.
| Восстановите по сохранившимся номерам путь коня, побывавшего по одному разу на всех клетках доски размером 6×6. (То есть расставьте числа от 1
до 36 так, чтобы отличающиеся на 1 были связаны ходом коня.)
| 17
| | | | 11 | |
| 2
| | | 25 | | |
| 23
| 16 | 1 | | | |
| 30
| | | 19 | | |
| 15
| | | | 13 | |
| 8
| | | | | 35 |
|
Указание I
Указание II
Ответ |
|
Указание I. Сначала подумайте, какое число стоит на поле, помеченном буквой а, затем — буквами б, в, и так далее.
| 17
| г | ж | | 11 |
б |
| 2
| | а | 25 | з | |
| 23
| 16 | 1 | е | в | д |
| 30
| м | | 19 | | и |
| 15
| | л | | 13 | |
| 8
| |
н
| | к | 35 | |
| |
|
Указание II. Подумайте теперь, какие числа стоят на полях, помеченных буквами о,
п, р.
| 17
| 24 | 3 | | 11 | 26 |
| 2
| | 18 | 25 | 4 | |
| 23
| 16 | 1 | 10 | 27 | 12 |
| 30
| 9 | | 19 | | 5 |
| 15
| р | 7 | | 13 |
о |
| 8
| | 14 | п
| 6 | 35 | |
| |
|
Ответ.
| 17
| 24 | 3 | 32 | 11 | 26 |
| 2
| 31 | 18 | 25 | 4 | 33 |
| 23
| 16 | 1 | 10 | 27 | 12 |
| 30
| 9 | 28 | 19 | 34 | 5 |
| 15
| 22 | 7 | 36 | 13 | 20 |
| 8
| 29 | 14 | 21 | 6 | 35 | | |
| | |
|
133.
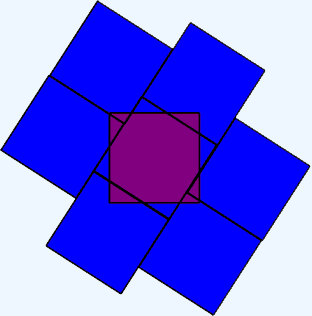
| Покройте семью синими квадратными ковриками красный квадратный коврик такого же размера так, чтобы синие коврики не налегали друг на друга, но каждый синий покрывал какую-то часть красного.
| Ответ |
|
Ответ.
| | | |
|
134.
| Дама сдавала в багаж диван, чемодан, саквояж, картину, корзину, картонку и маленькую собачонку. Диван весил столько же, сколько чемодан и саквояж, вместе взятые, и столько же, сколько картина, корзина и картонка вместе. Картина, корзина и картонка весили поровну; каждая из них весила больше, чем собачонка. Когда выгружали багаж, дама заявила, что собака не той породы. При проверке оказалось, что собака перевешивает диван, если к ней на весы добавить саквояж или чемодан. Докажите, что претензия дамы была справедлива.
|
Указание
Решение
Комментарий |
|
|
|
Указание. Обозначьте массы предметов их первыми буквами: Д (диван), Ч (чемодан), С (саквояж), К (картина, корзина, картонка), а массу маленькой собачонки — буквой М.
Запишите условие задачи в виде системы равенств и неравенств:
Д = Ч + С,
Д = 3К,
К > М,
М + С > Д,
М + Ч > Д. |
| |
|
Решение. Записав условие задачи так, как сказано в указании, и сложив неравенства
М + С > Д
и
М + Ч > Д,
вследствие равенства
Ч + С = Д
получаем неравенство
2М > Д.
С другой стороны,
Д = 3К > 3М.
Получили противоречие:
2М > Д > 3М. |
|
|
|
Комментарий. Верна следующая теорема: система линейных неравенств несовместна тогда и только тогда, когда существует линейная комбинация этих неравенств с положительными коэффициентами, являющаяся неверным числовым неравенством.
Посмотрим, как проявляет себя утверждение этой теоремы в нашей задаче. Исключив Ч и К, условие запишем в виде следующей системы неравенств:
Д – 3М > 0,
М + С – Д > 0,
М – С > 0,
М > 0,
Д > 0,
С > 0.
Сложив первые четыре из этих неравенств, получаем
(Д – 3М) + (М + С – Д)
+ (М – С) + М > 0,
то есть 0 > 0.
Замечания. Подробнее о неравенствах первой степени можно прочитать в книге А.С. Солодовникова «Системы линейных неравенств».
Эта задача заимствована из книги Н.Б. Васильева, В.Л. Гутенмахера, Ж.М. Раббота и А.Л. Тоома «Заочные математические олимпиады». В ней сказано: «В 1979 году московский математик Л.Г. Хачиян заметил, что алгоритм выяснения совместности системы линейных неравенств, основанный на совсем другой идее («дихотомии»), допускает полиномиальную оценку сложности (в отличие от симплекс-метода, сложность которого экспоненциальна).» |
| | |
|
135.
| Три человека — A, B и C — пересчитали кучу шариков четырёх цветов. Каждый из них правильно различал два цвета, а два других не различал: кто-то один из них не различал красный и оранжевый, другой не различал оранжевый и жёлтый, а ещё один не различал жёлтый и зелёный. Глядя на таблицу, узнайте, сколько каких шариков было.
| | красный | оранжевый | жёлтый | зелёный |
| A | 2 | 5 | 7 | 9 |
| В | 2 | 4 | 9 | 8 |
| C | 4 | 2 | 8 | 9 |
|
Ответ
Указание |
|
Ответ. 2 красных, 4 оранжевых, 8 жёлтых и 9 зелёных.
| | |
Указание. Поскольку красные шарики путал с оранжевыми только один человек, то было 2 красных шарика, а C путал красные с оранжевыми.
| | | |
|
136.
| Первая слева цифра десятизначного числа равна числу единиц в записи этого числа, вторая — числу двоек, третья — числу троек, четвёртая — числу четвёрок,..., девятая — числу девяток, десятая — числу нулей. Придумайте такое число.
|
|
137.
| На рисунке показаны три способа расставить на шахматной доске 24 коня, каждый из которых бьёт двух других. Расставьте на доске 32 коня, чтобы каждый из них бил ровно двух других.

|
Указание
Ответ |
|
Указание. Разрежьте доску на четыре доски размером 4×4.
| | |
Ответ. На каждой из четвертей в углу разместим 8 коней в виде квадрата 3×3:

| | | |
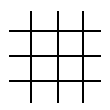 а) На рисунке 6 отрезков расположены так, что каждый пересекает три других отрезка. Расположите
а) На рисунке 6 отрезков расположены так, что каждый пересекает три других отрезка. Расположите 




