Семь задач

Ответ

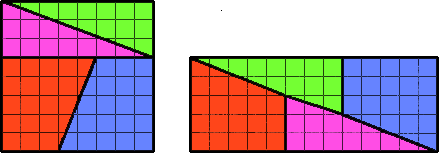
Ответ. Диагональная линия левого рисунка не прямая; на точном рисунке виден параллелограмм площади 1, как и следовало ожидать. Последовательность Фибоначчи j1 = 1, j2 = 1, j3 = 2, j4 = 3, j5 = 5, j6 = 8, j7 = 13, j8 = 21, j9 = 34, j10 = 55, j11 = 89, ... обладает следующим свойством: квадрат числа Фибоначчи на 1 отличается от произведения предшествующего ему и следующего за ним чисел Фибоначчи; точнее говоря, jn2 + (–1)n = jn – 1jn + 1. Например, при n = 6 формула превращается в равенство 82 + 1 = 5 · 13, а при n = 7 — в равенство 132 – 1 = 8 · 21. Советую нарисовать картинки, аналогичные рисунку к условию задачи, для нескольких других значений n.

219.	Из 40 спичек образована квадратная решётка (каждая сторона маленького квадратика — одна спичка). Снимите 9 спичек, чтобы полностью не сохранилось контура ни одного квадрата (состоящего из одного или большего количества маленьких квадратиков). (Достаточно указать один способ, как это сделать.) Пояснение   Ответ Пояснение. На нижеследующем рисунке убраны 9 спичек. Полностью сохранился контур только одного квадрата: Ответ.
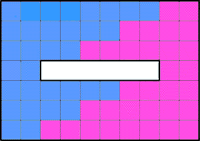
220.	Из прямоугольника размером 10×7 вырезали прямоугольник 1×6, как показано на рисунке. Разрежьте полученную фигуру на две конгруэнтные (одинаковые и по площади, и по форме) части, из которых можно сложить квадрат. Ответ Ответ.
221.	Решите ребусы: а) УМ + ШУМ = ВМШ; б) ДУРАК + УДАР = ДРАКА; в) ОДИН + ОДИН = МНОГО; г) FORTY + TEN + TEN = SIXTY.
222.	Известно, что a и b — натуральные числа, а из следующих четырёх утверждений — a + 1 делится на b, a = 2 b + 5, a + b делится на 3, a + 7b — простое число, — три верных, а одно неверное. Найдите все возможные пары чисел a, b. Ответ   Указание   Решение Ответ. a = 9, b = 2 или a = 17, b = 6. Указание. Докажите сначала несовместность второго и третьего условий; затем докажите несовместность третьего и четвёртого условий. Решение. Пусть a = 2b + 5. Тогда a + b = 3b + 5 не делится на 3. Следовательно, второе и третье условия несовместны. Далее, предположим, что число a + b делится на 3. Тогда a + 7b = (a + b) + 6b делится на 3 и, поскольку a + 7b > 3, не может быть простым числом. Мы доказали несовместность третьего и четвёртого условий. Следовательно, третье условие ложно, а остальные три истинны. В частности, a = 2b + 5. Подставив это выражение в первое условие, видим: 2b + 6 делится на b, так что число b является делителем числа 6. Проще говоря, b = 1, 2, 3 или 6. Рассмотрим теперь следующую таблицу: b 1 2 3 6 a 7 9 11 17 a + 7b 14 23 32 59 Ответ теперь очевиден: b = 2, a = 9 или b = 6, a = 17.
223.	Илье Муромцу, Добрыне Никитичу и Алёше Поповичу за верную службу дали 6 монет: 3 золотые и 3 серебряные. Каждому досталось по две монеты. Илья Муромец не знает, какие монеты достались Добрыне, а какие Алёше, но знает, какие монеты достались ему самому. Придумайте вопрос, на который Илья Муромец ответит «да», «нет» или «не знаю» и по ответу на который Вы сможете понять, какие монеты ему достались. Решение Решение. Вопрос может звучать так: «Верно ли, что и Алёше Поповичу, и Добрыне Никитичу досталось хотя бы по одной серебряной монете?» Если ответ утвердительный, то обе монеты Ильи Муромца — золотые. Если отрицательный, то Илье достались две серебряные монеты. А если Илья не сможет ответить ни «да», ни «нет», то он получил за службу золотую и серебряную монеты. Можно было задать и другие вопросы, например: — Верно ли, что хотя бы одному из двух других богатырей достались две серебряные монеты? — У тебя больше золотых монет, чем у Алёши Поповича? — Если я заберу одну из твоих монет и дам вместо неё золотую, то станет ли у тебя больше золотых? (Заметьте, что в этом вопросе не упомянуты монеты, доставшиеся двум другим богатырям!)
224.	Нарисуйте на клетчатой бумаге прямоугольник шириной 33 и высотой 32 клетки и разрежьте его на квадраты, как показано на рисунке. (Резать можно только вдоль линий сетки!)