Котёнок, Коперник и астроида

Рассказ пойдёт о падающей лестнице, теореме Коперника и об астроиде. Оказывается, это почти одно и то же! Если пожелаете познакомиться со всем этим подробнее, обратитесь к книге «Прямые и кривые» Н.Б. Васильева и В.Л. Гутенмахера.

Котёнок на лестнице

Как-то раз сидел маленький котёнок на лестнице. В точности в её середине.

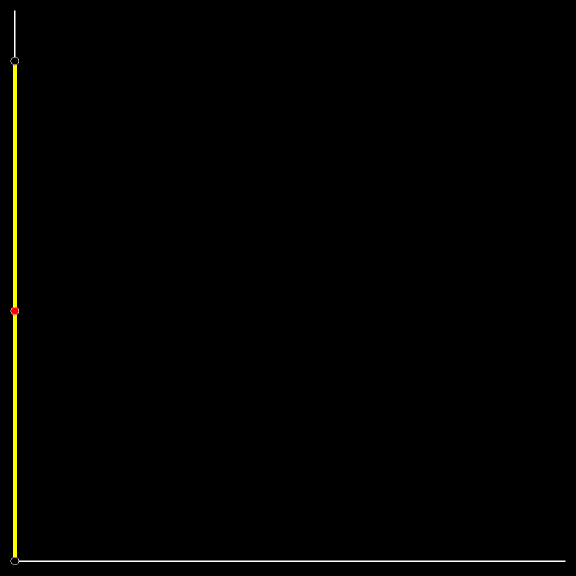В начале лестница стояла строго вертикально, обоими концами у стены.

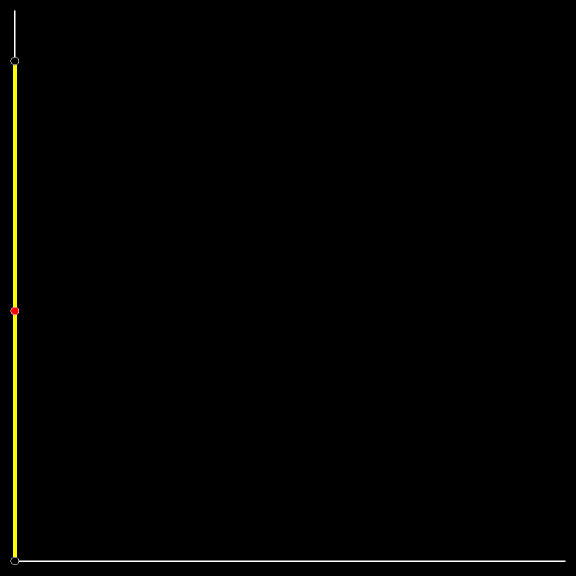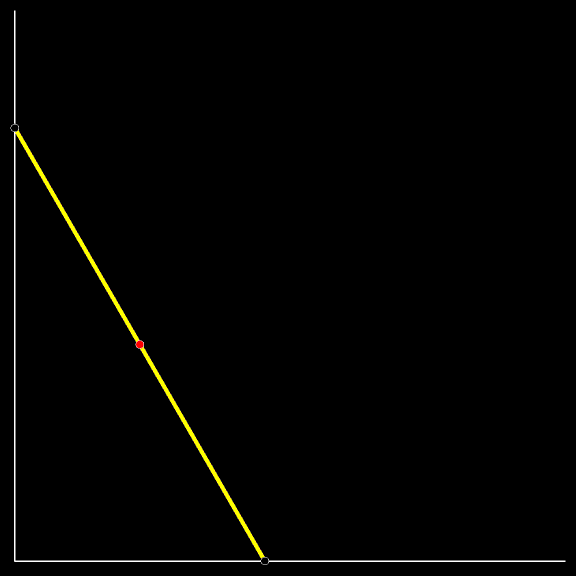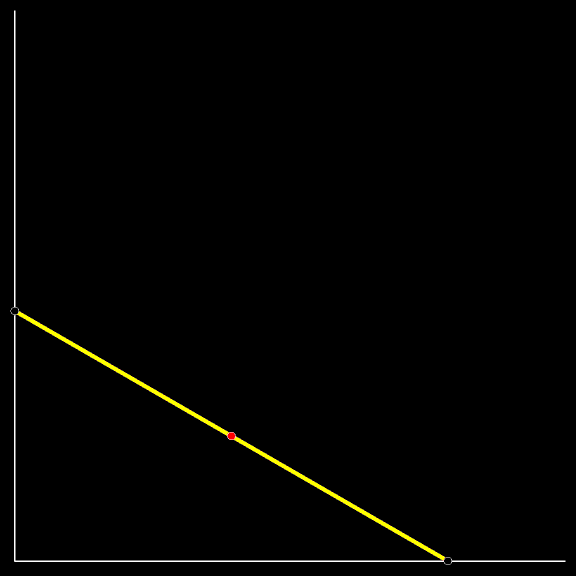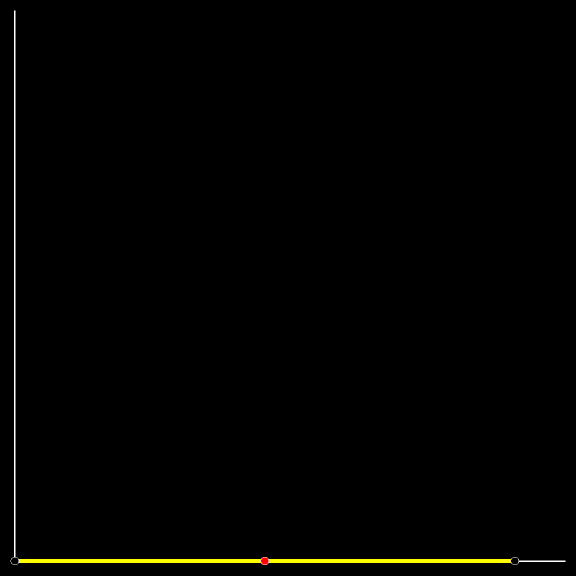Вертикальное положение весьма неустойчиво. Вот лестница и упала. Падала она так, что верхний её конец спускался сверху вниз по вертикальной стене, а нижний скользил по земле. Проследите за траекторией красной точки — середины лестницы.

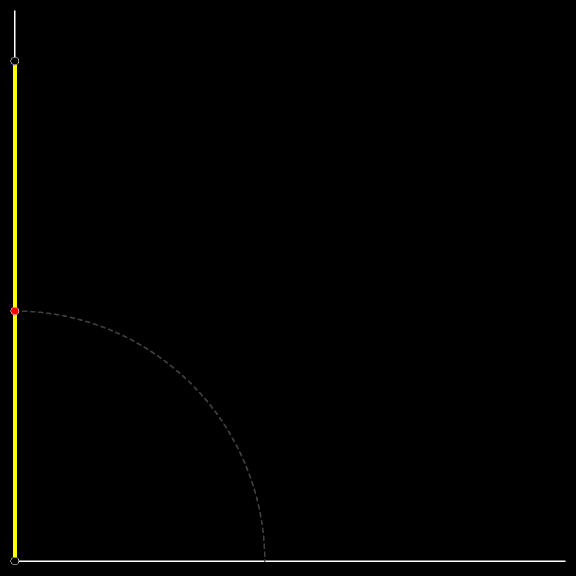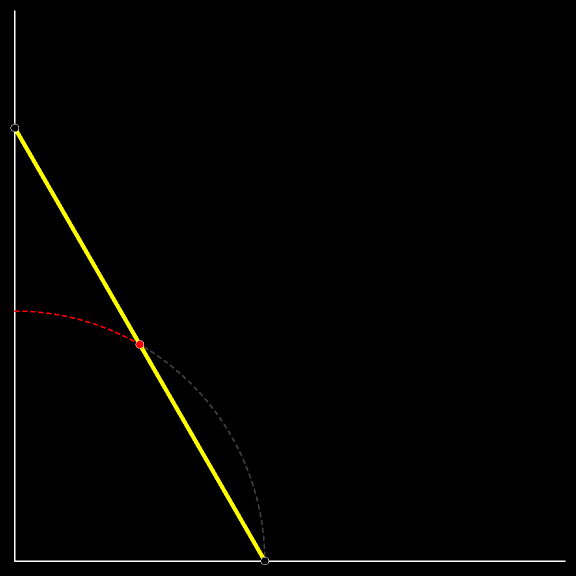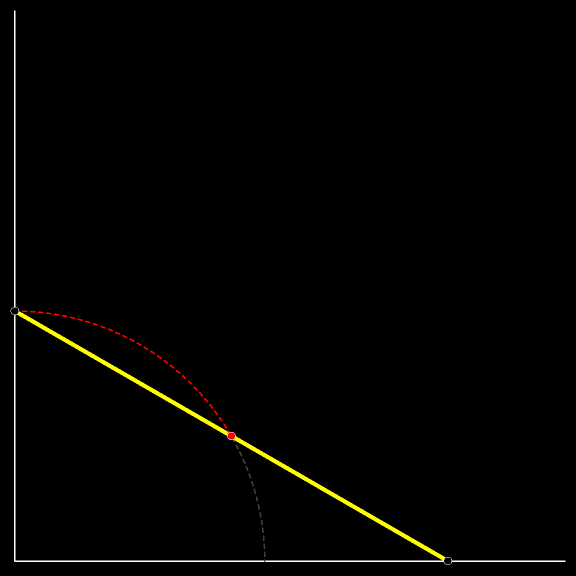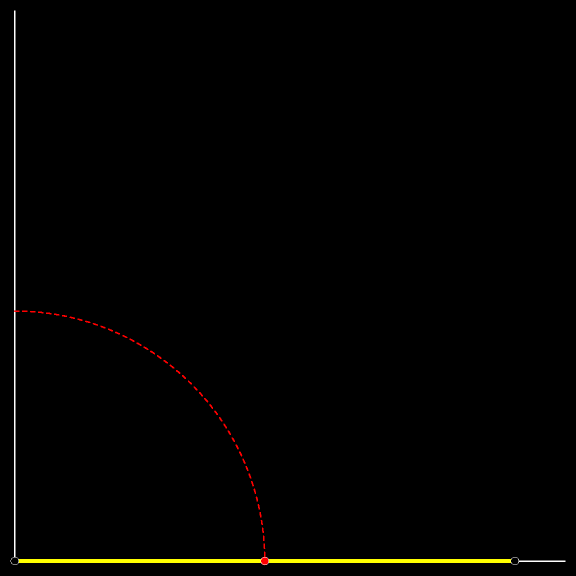Это дуга окружности. Её центр — вершина прямого угла.

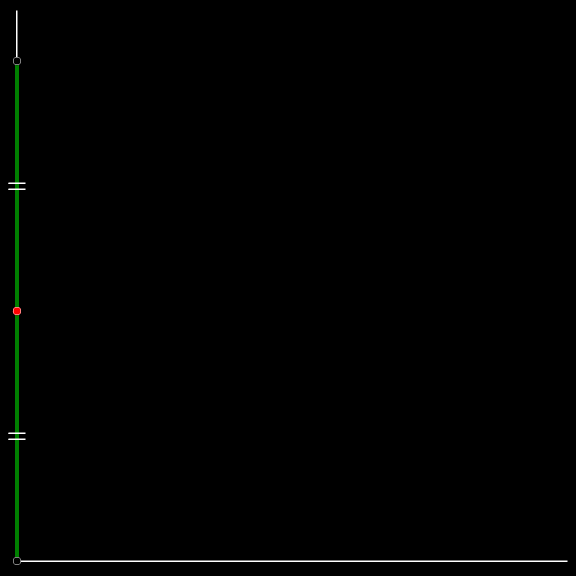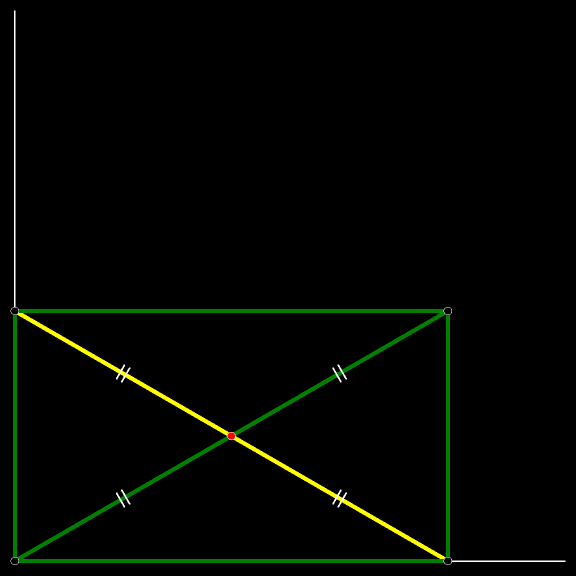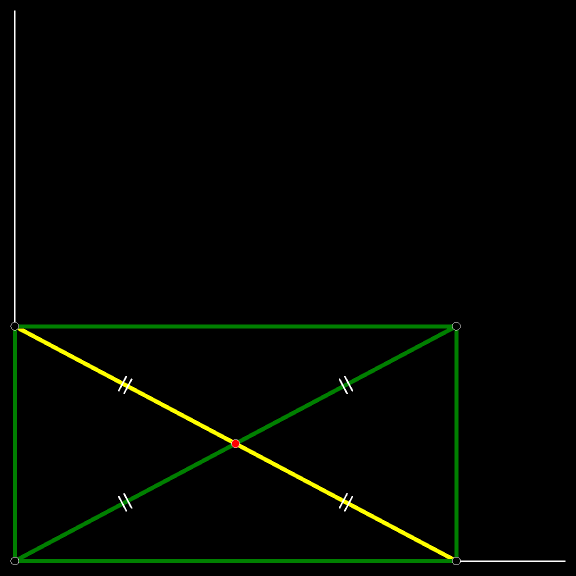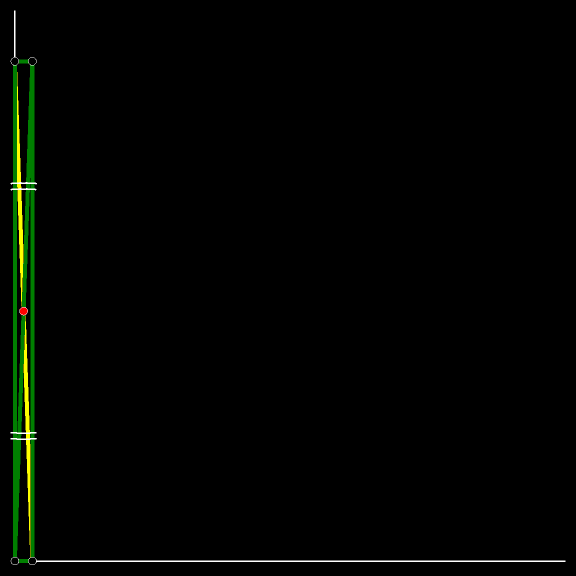Доказательство: диагонали прямоугольника точкой пересечения делятся пополам; расстояние от вершины прямоугольника до котёнка — то есть до точки пересечения диагоналей прямоугольника — равно половине диагонали. (Подумайте, как падал бы котёнок, если бы нижний конец лестницы застрял в вершине прямого угла. Два способа падения лестницы — две диагонали прямоугольника! Траектория котёнка одна и та же, только при одном способе падения котёнок в последний момент оказывается над лестницей, а при другом — под лестницей.) Мы доказали, что медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.

Теорема Коперника

Рассмотрим окружность.

Внутри неё расположим окружность вдвое меньшего радиуса так, чтобы эти две окружности — большая и маленькая — касались. Поскольку диаметр меньшей окружности равен радиусу исходной, то меньшая окружность проходит через центр исходной окружности.

Отметим на меньшей окружности произвольную точку.

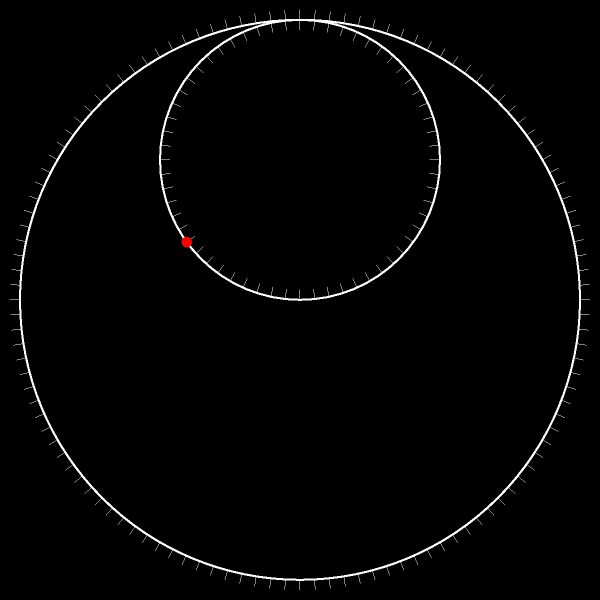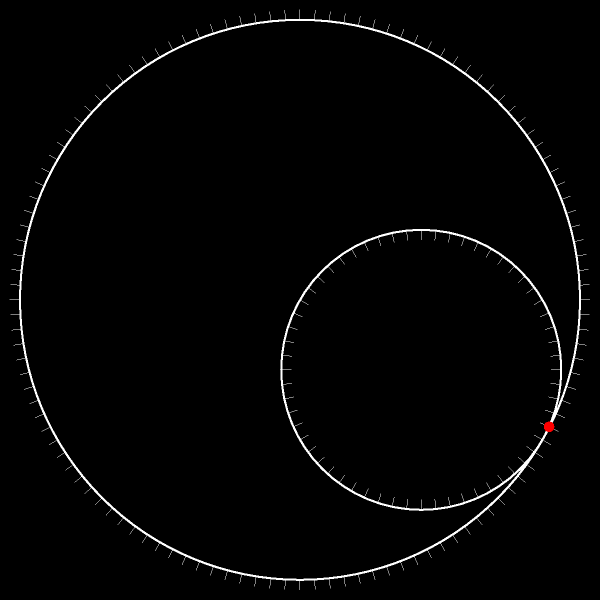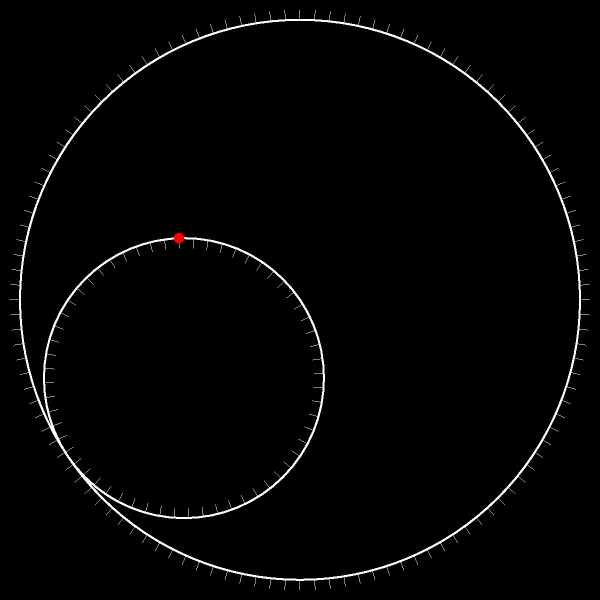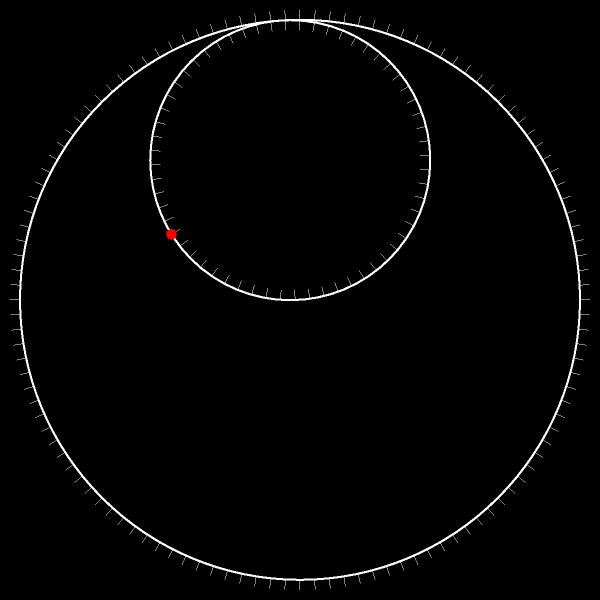Пусть меньшая окружность движется без проскальзывания по неподвижной исходной окружности. Проследите за траекторией отмеченной точки!

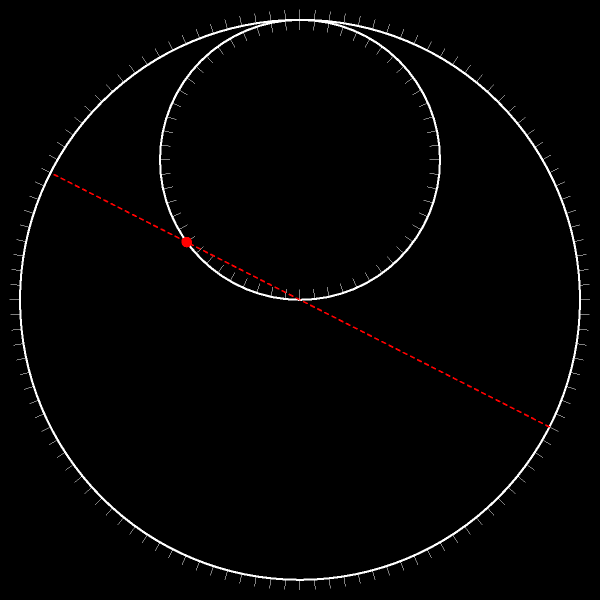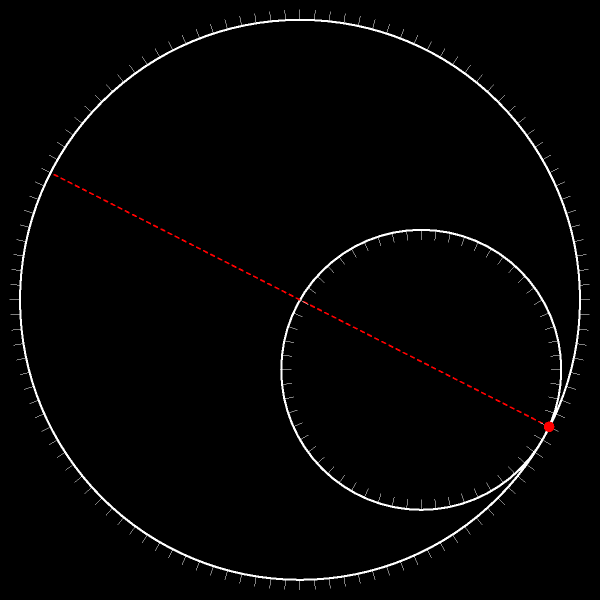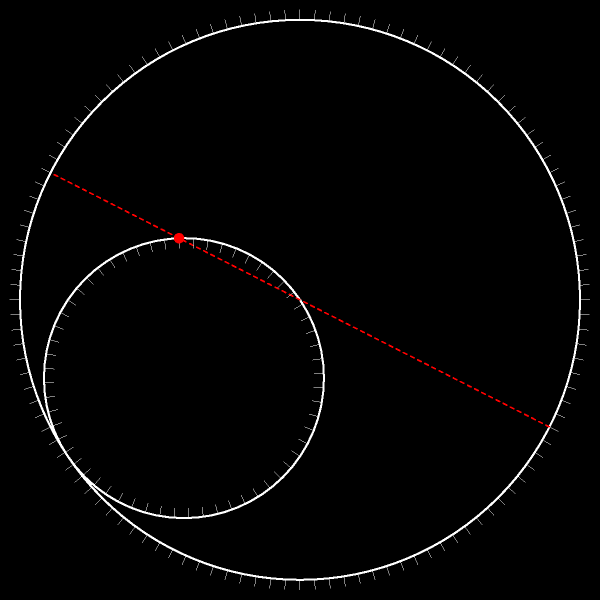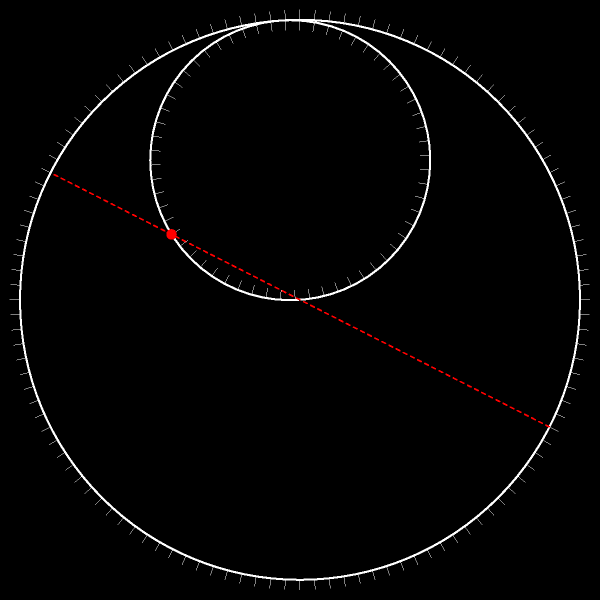Траектория — диаметр исходной окружности!

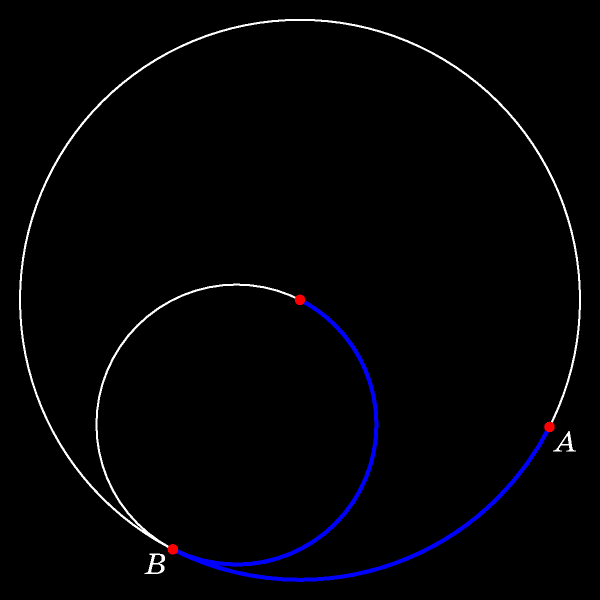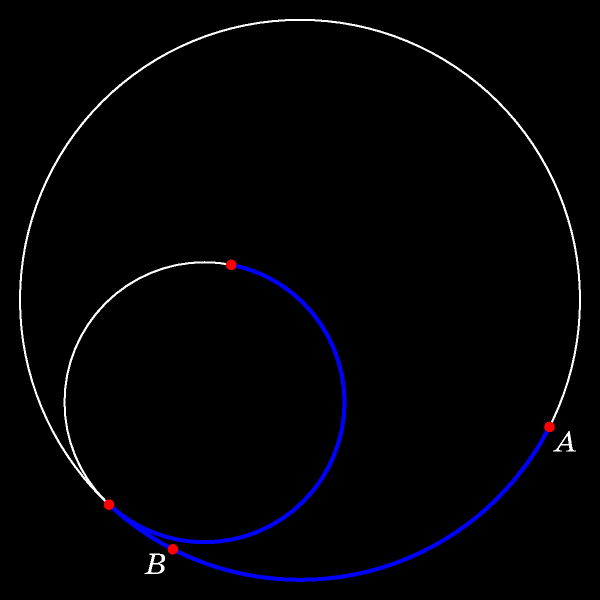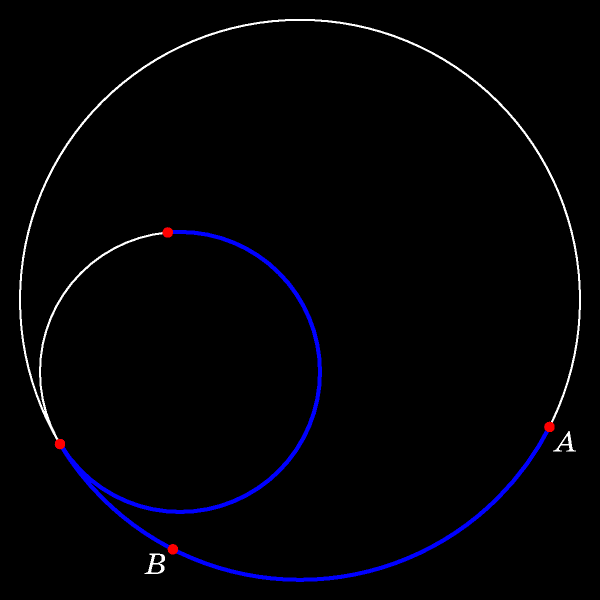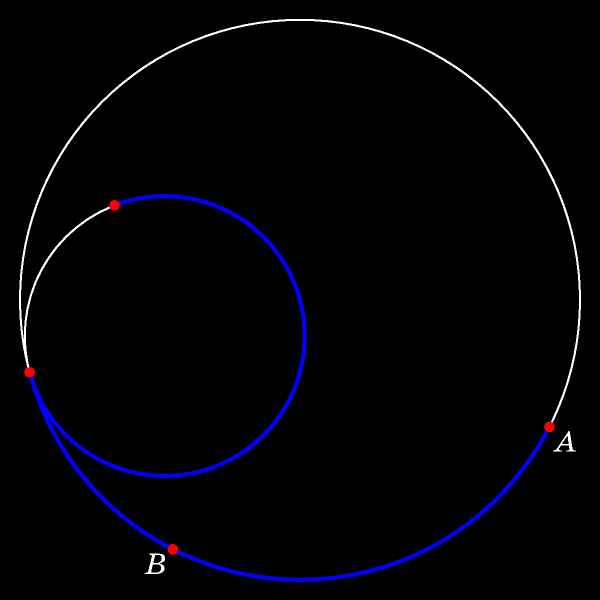
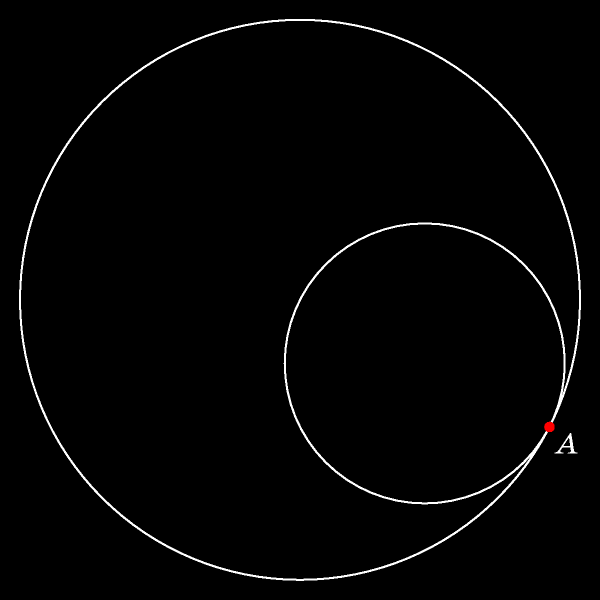Чтобы доказать эту теорему, дождёмся момента, когда отмеченная точка окажется точкой касания движущейся и неподвижной окружностей, и обозначим эту точку буквой A.

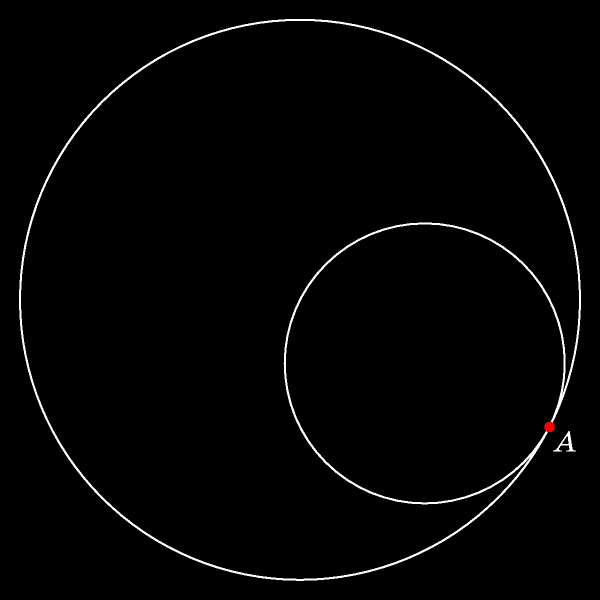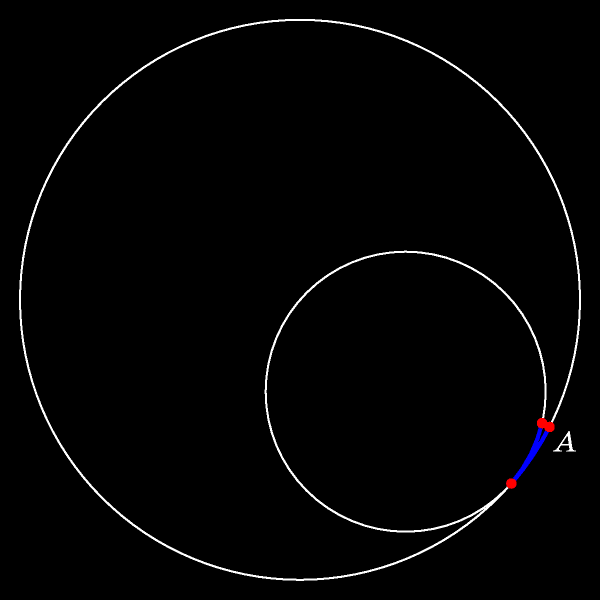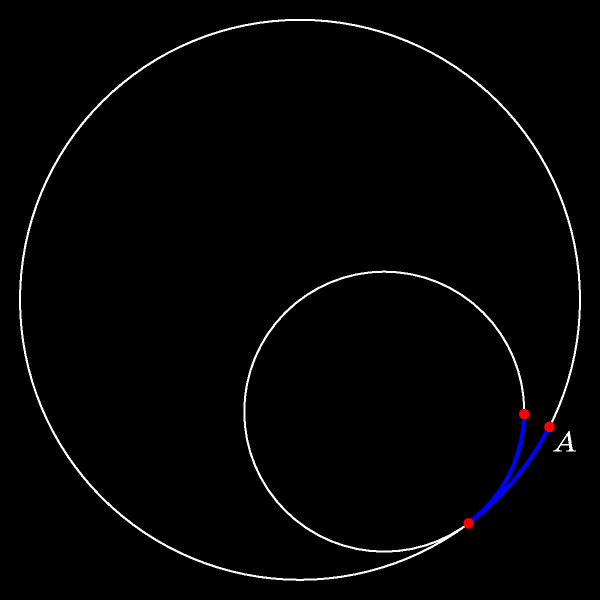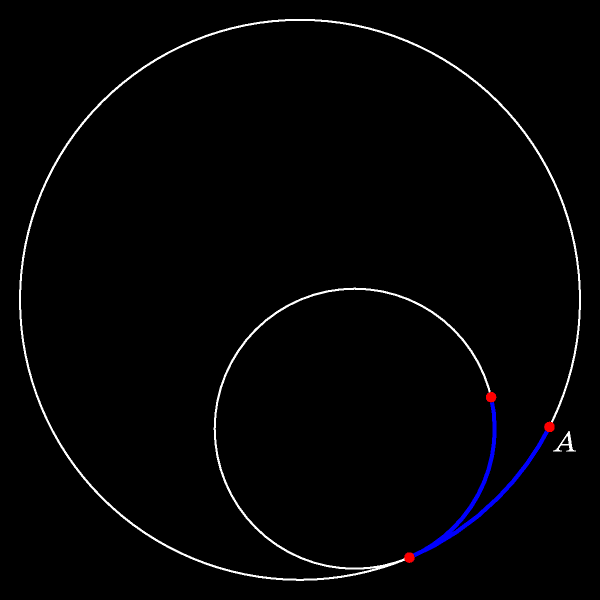В процессе движения отмеченная точка сдвинется с неподвижной окружности внутрь круга. Длины прокатившихся одна по другой дуг (синих на рисунке) равны — движение происходит без проскальзывания. (В доказательстве это не нуждается, поскольку движение без проскальзывания — это и есть движение, при котором длины прокатившихся одна по другой дуг равны.)

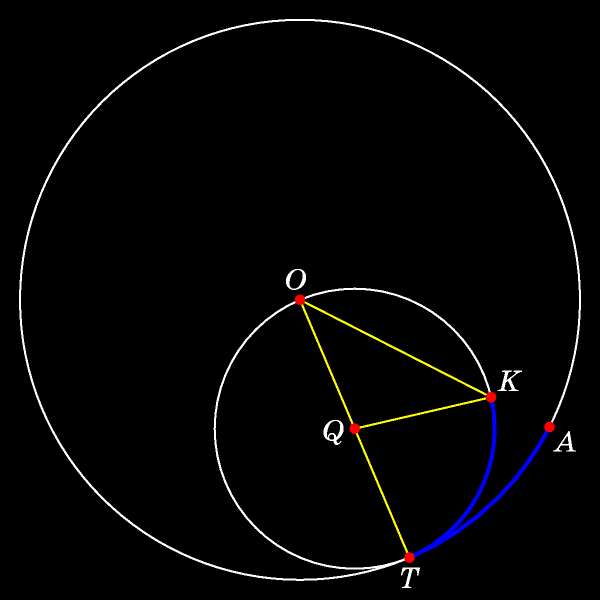По теореме о вписанном угле величина угла TQK в два раза больше величины угла TOK. Поскольку радиус меньшей окружности в два раза меньше радиуса неподвижной окружности, то угол TOK высекает на неподвижной окружности дугу той же длины, что и дуга, высекаемая на окружности вдвое меньшего радиуса вдвое большим углом TQK. Это и означает, что точка K лежит на отрезке OA.

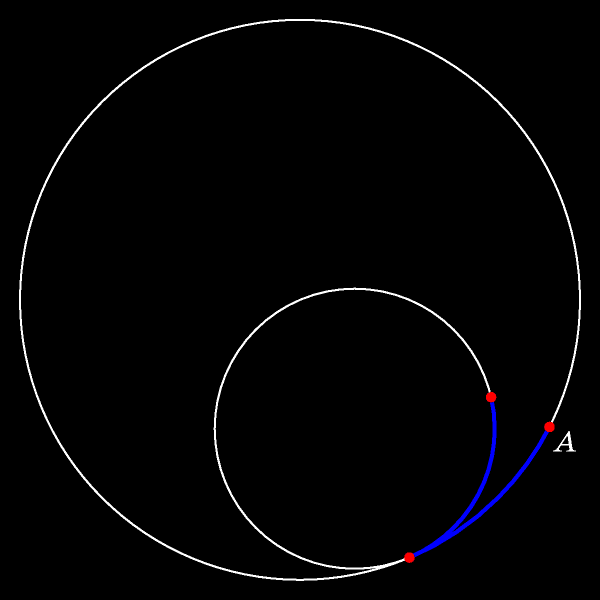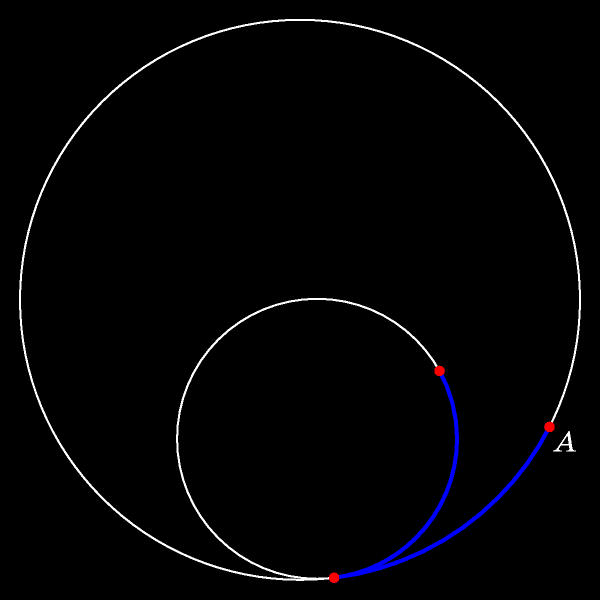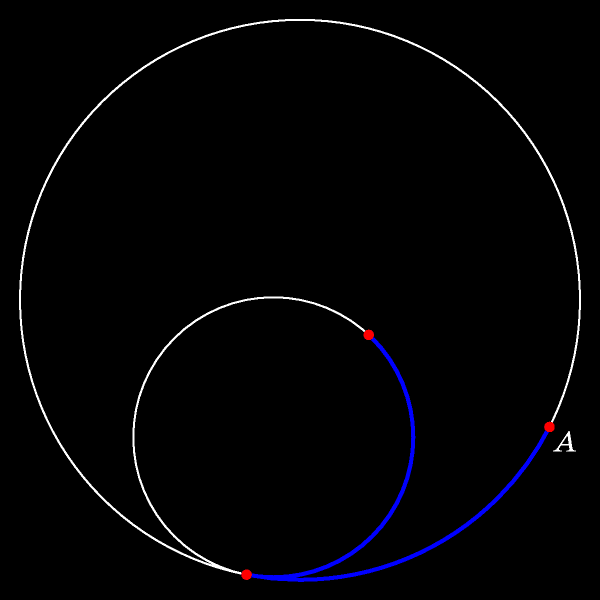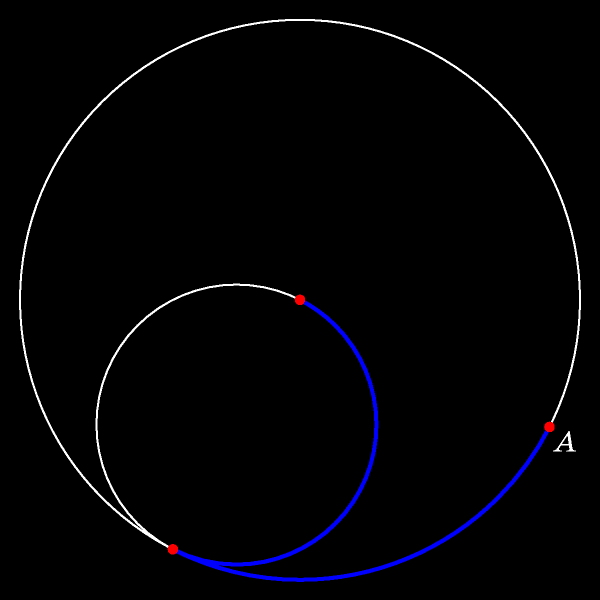В некоторый момент отмеченная точка окажется в центре неподвижной окружности. К этому моменту половина меньшей окружности прокатилась по четверти неподвижной окружности.

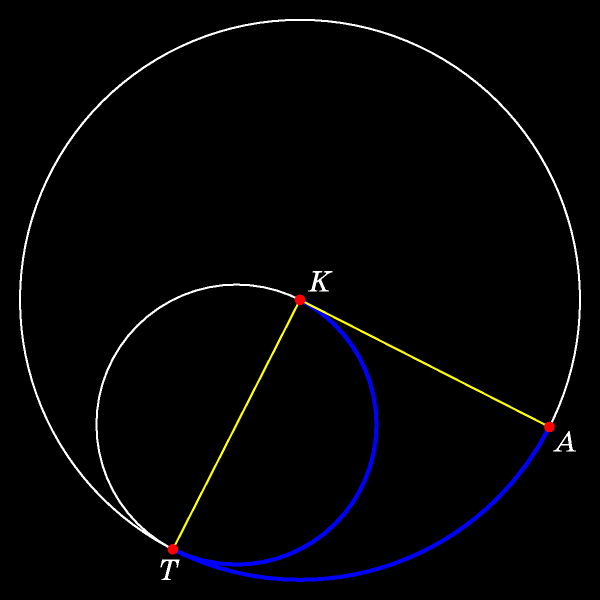В этот момент времени угол TAK прямой.

Смотрите, как расположены точки после того, отмеченная точка прошла через центр неподвижного круга.

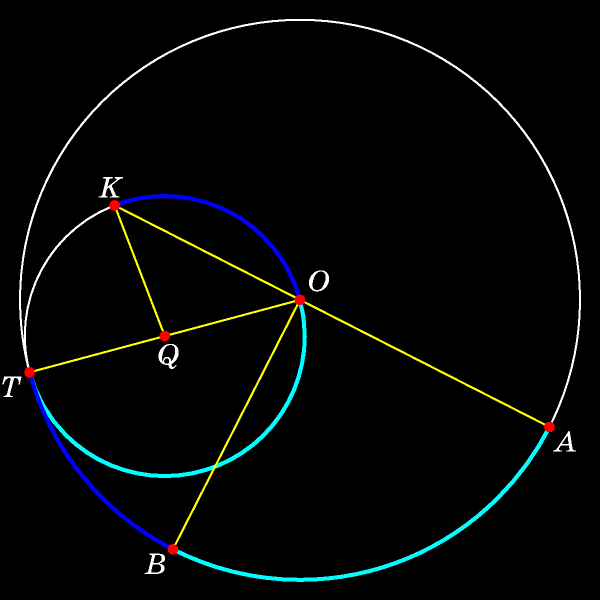Поскольку движение происходило без проскальзывания, то длина белой дуги TK равна длине дуги, дополняющей синюю и голубую дуги неподвижной окружности до полуокружности. Таким образом этот случай сводится к уже рассмотренному случаю теоремы Коперника. (На рисунке равны длины синих дуг; равны и длины голубых дуг.)

Теорема Коперника доказана!

Прямоугольный треугольник и лестница

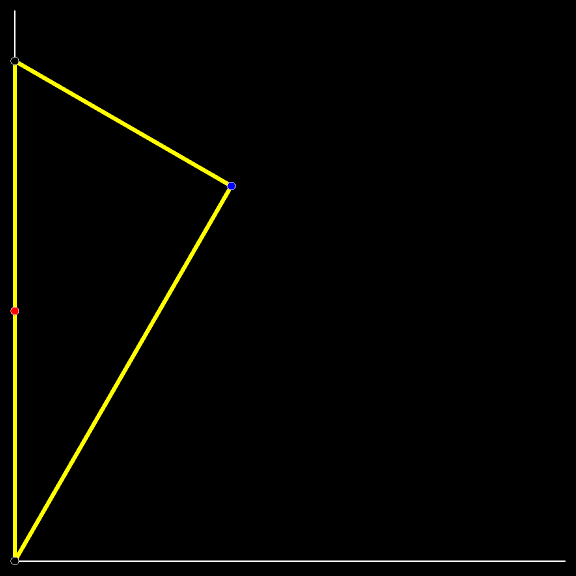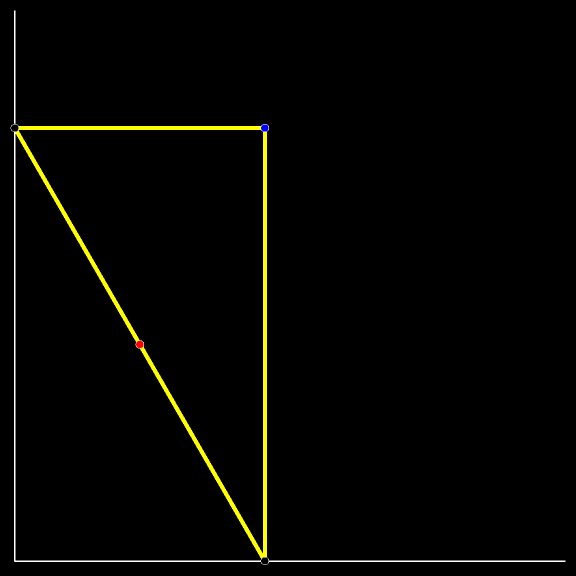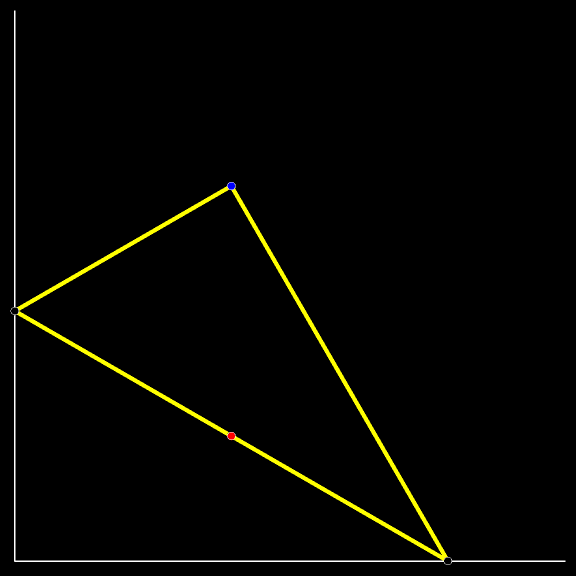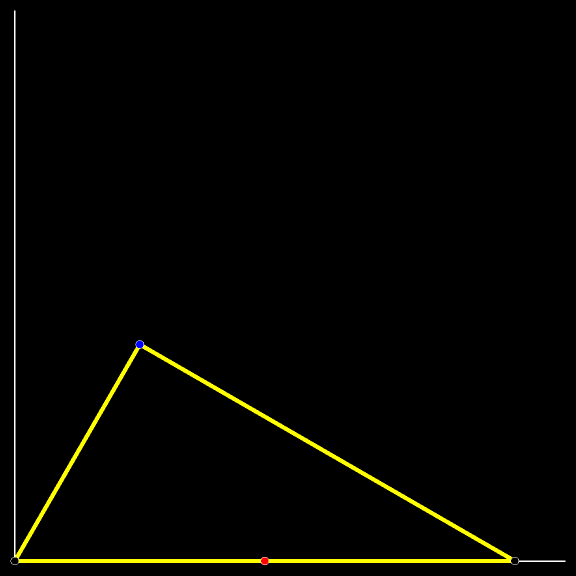Мы уже изучили траекторию котёнка, сидящего в середине падающей лестницы. Заменим котёнка на прямоугольный треугольник, гипотенузой которого является лестница. Проследите за траекторией синей точки — вершины прямого угла движущегося треугольника!

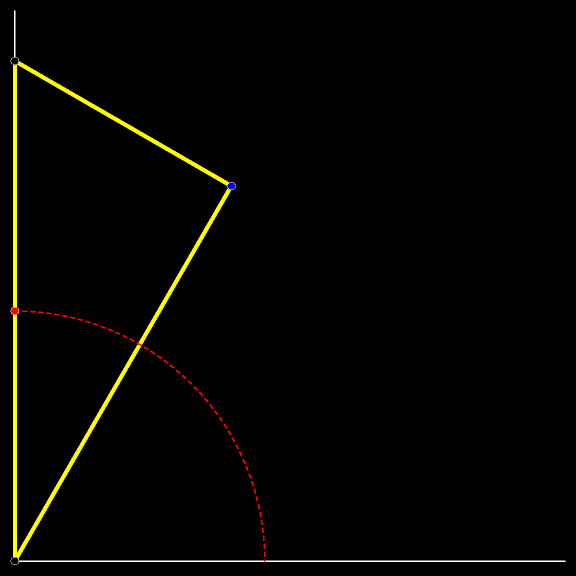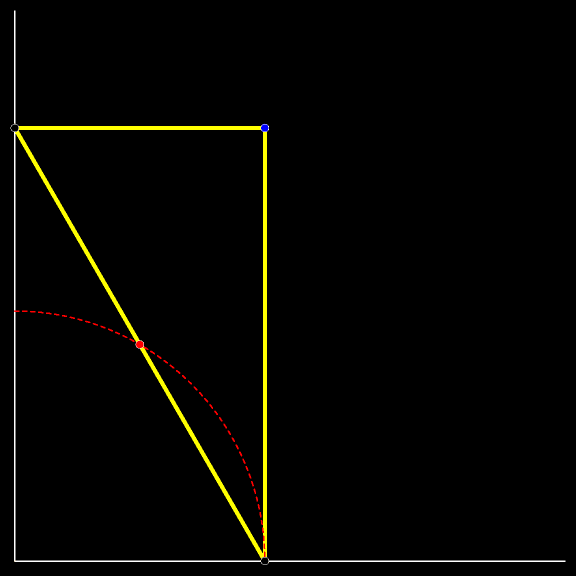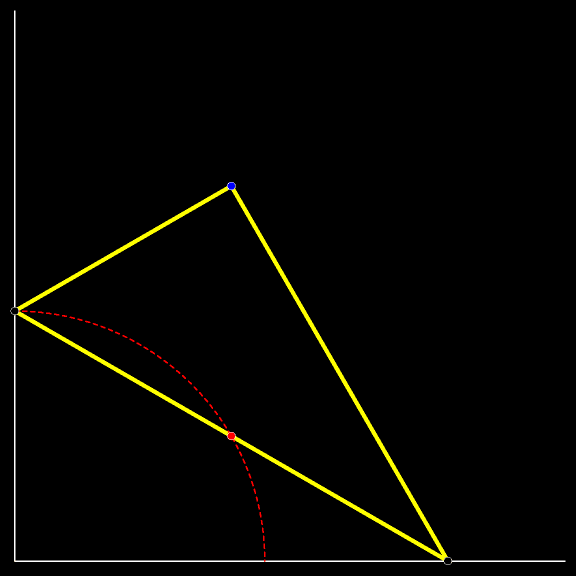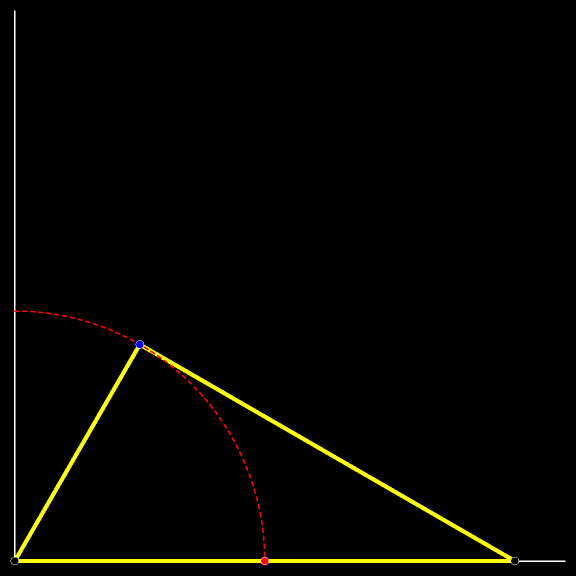Величины острых углов подвижного треугольника — 30 и 60 градусов, поэтому его меньший катет равен половине гипотенузы (читателям, которые забыли или никогда не знали доказательство этого факта, напоминаю: такой прямоугольный треугольник является половиной равностороннего треугольника). Только по этой случайной причине (не обязательно величины углов треугольника именно таковы!) в завершающий момент падения синяя точка оказывается на красной пунктирной окружности.

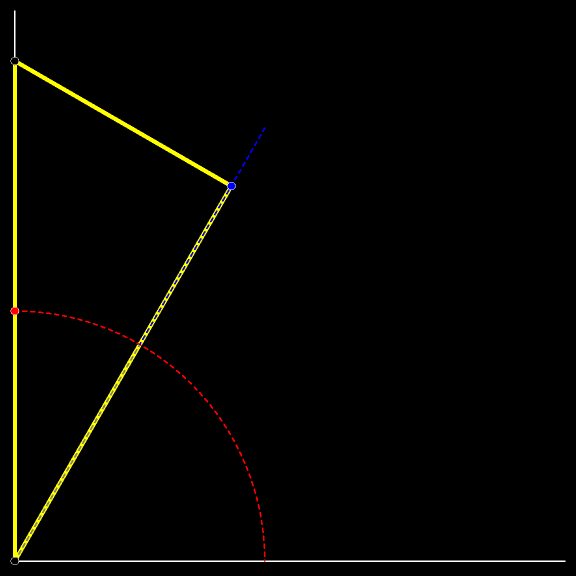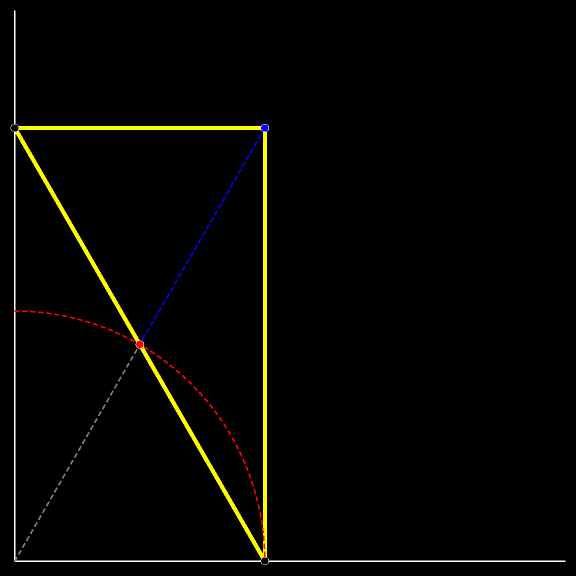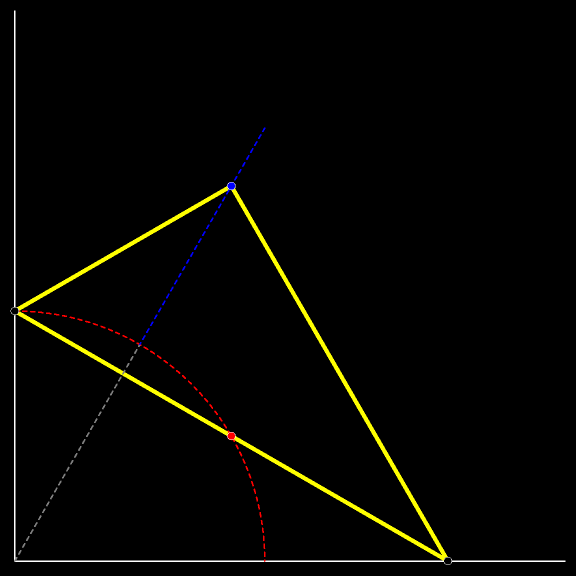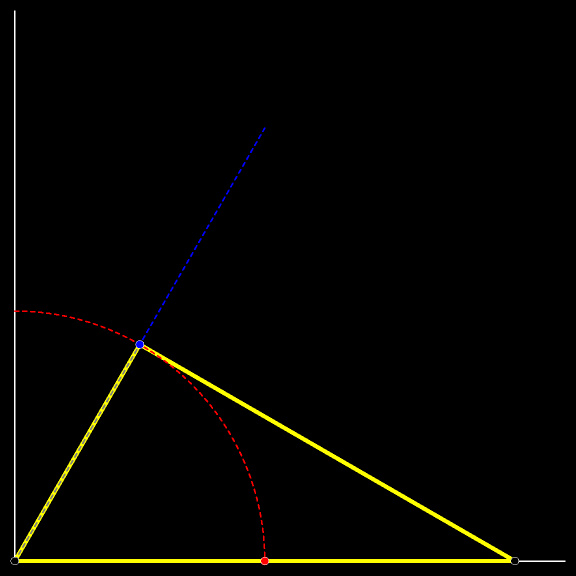Траектория вершины прямого угла движущегося треугольника — отрезок! Тому, что его конец оказался на траектории середины гипотенузы, мы всецело обязаны величинам углов движущегося прямоугольного треугольника. А тому, что это отрезок, а не более сложная линия,— теореме о вписанном угле.

В каждый момент движения существует окружность, проходящая через вершины движущегося треугольника и вершину неподвижного прямого угла (образованного стеной и полом). В самом деле, к каждому из двух прямоугольных треугольников, обладающих общей биссектрисой, применима теорема о том, что вершина прямого угла лежит на окружности, построенной на гипотенузе как на диаметре (другими словами, что проведённая из вершины прямого угла к гипотенузе медиана равна половине гипотенузы). Вследствие этой теоремы середина лестницы в процессе движения удалена от вершин обоих прямых углов на расстояние, равное половине длины лестницы.

Выделенные углы опираются на одну и ту же дугу окружности; следовательно, их величины равны. Поскольку в процессе движения величины углов движущегося треугольника не меняются, то отмеченный неподвижный угол неизменен; а это и означает, что траектория — отрезок.

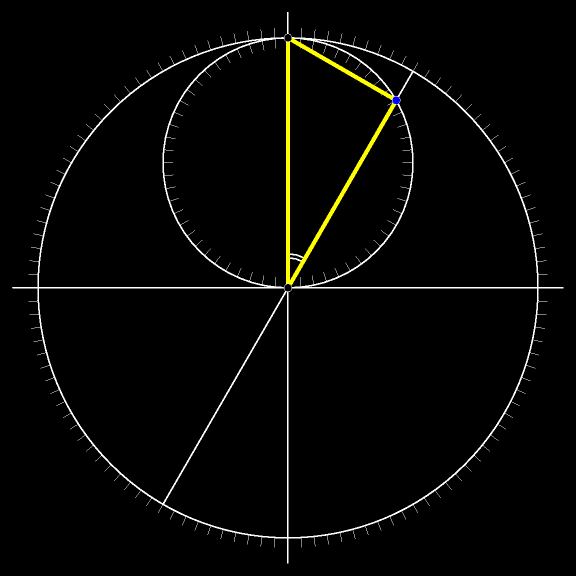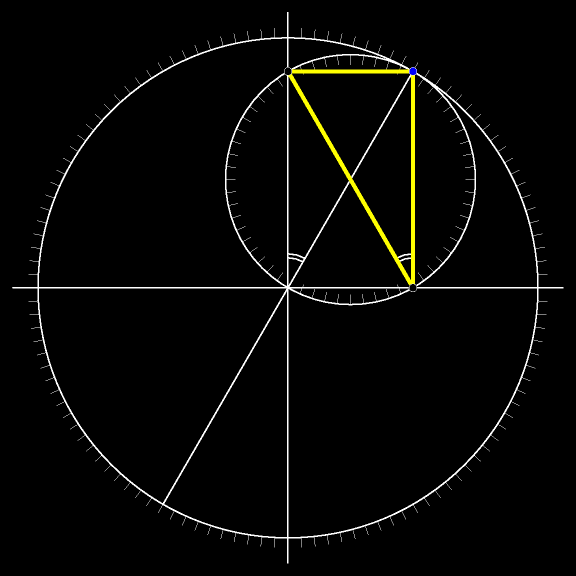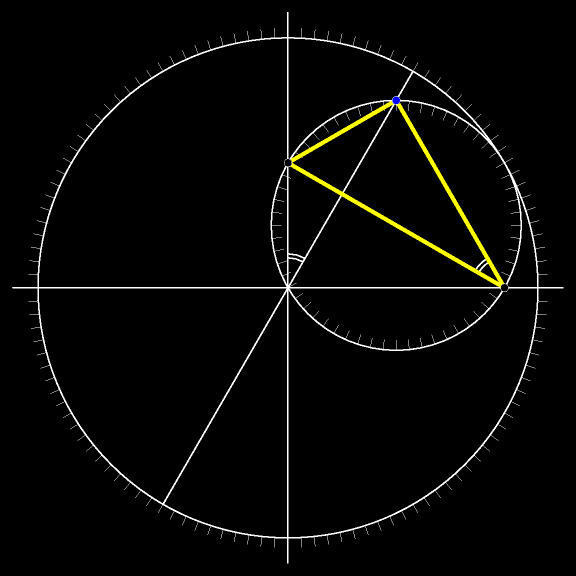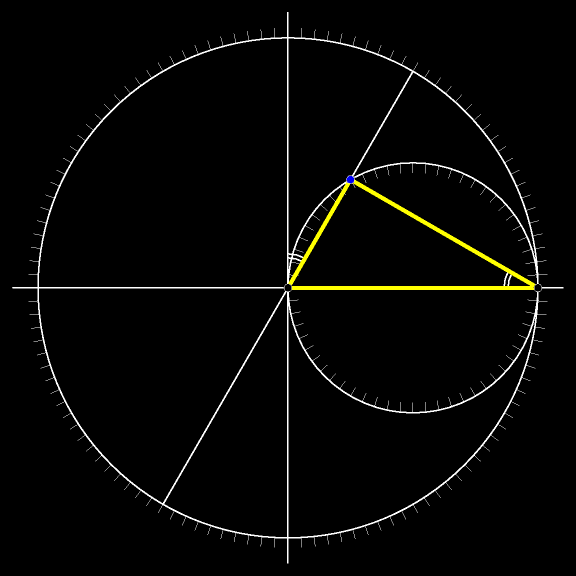Добавим к рассматриваемому рисунку окружность с центром в вершине неподвижного прямого угла и радиуом, равным длине лестницы. Очевидно, все три вершины движущегося треугольника участвуют в том самом движении, о котором говорит теорема Коперника: каждая — по своему диаметру неподвижной окружности.

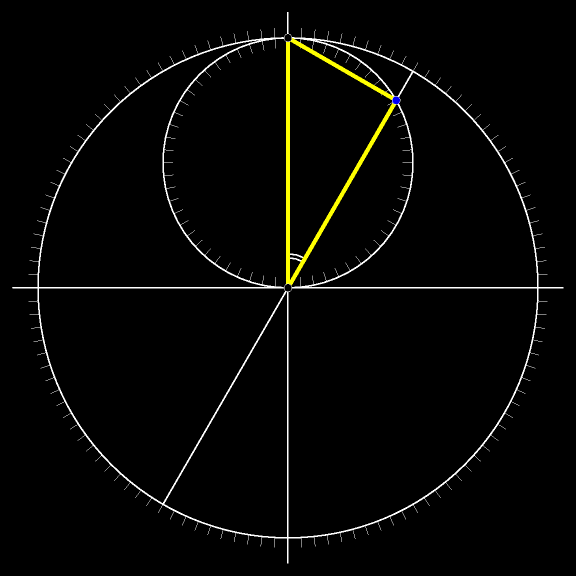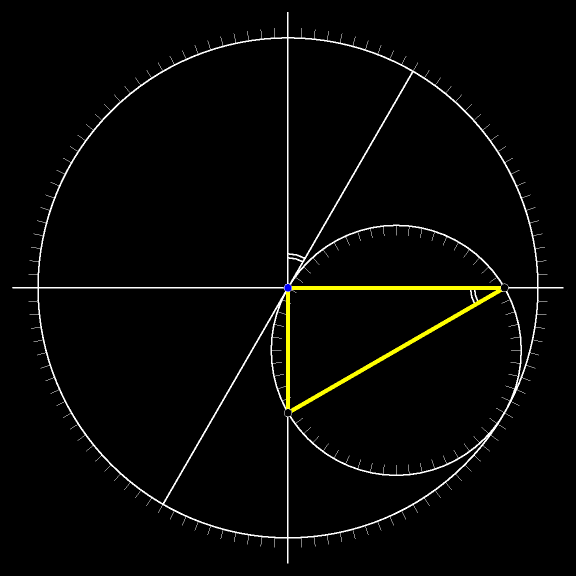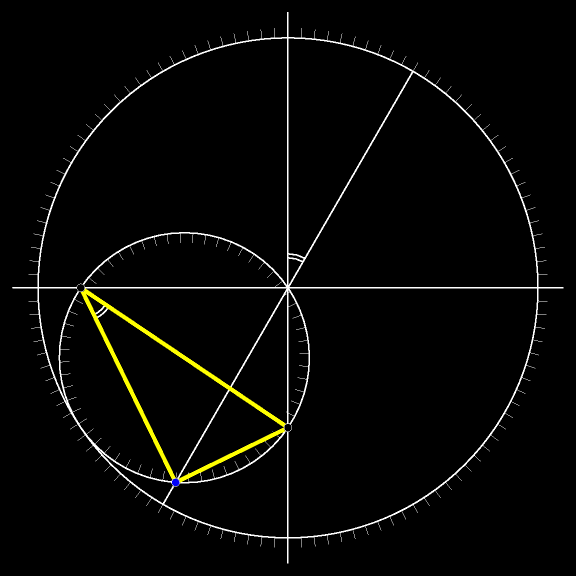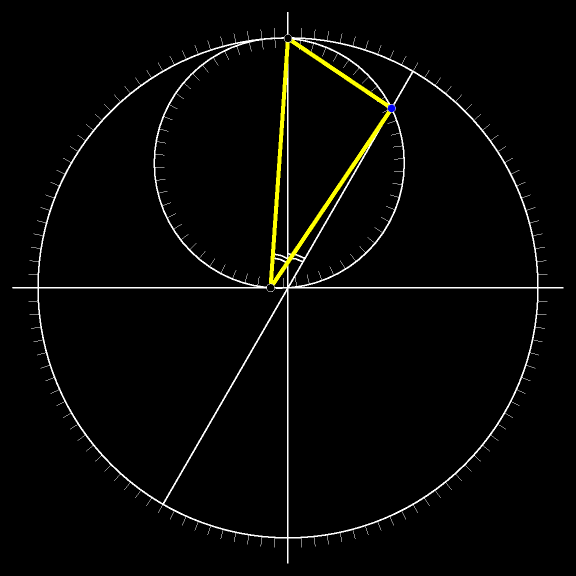Движение не обязательно ограничивать одним квадрантом: точки могут пробегать соответствующие диаметры окружностей целиком.

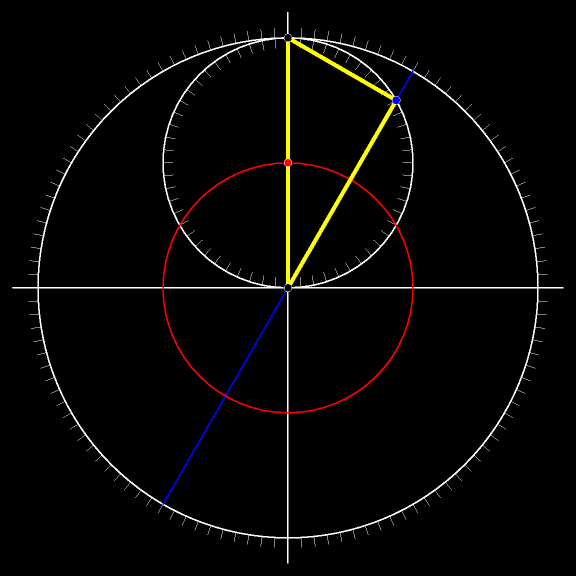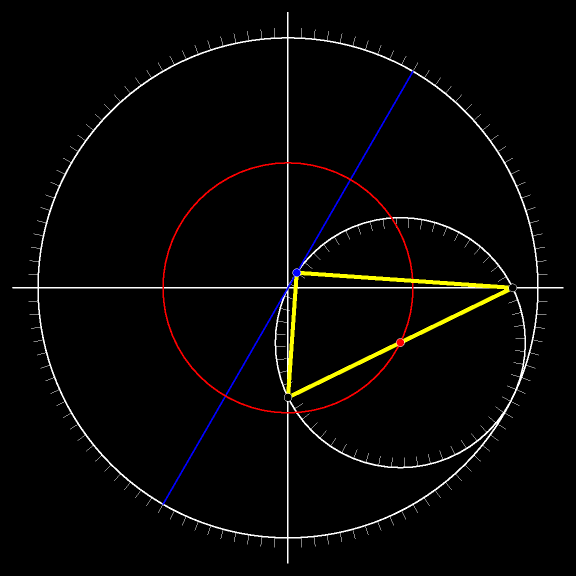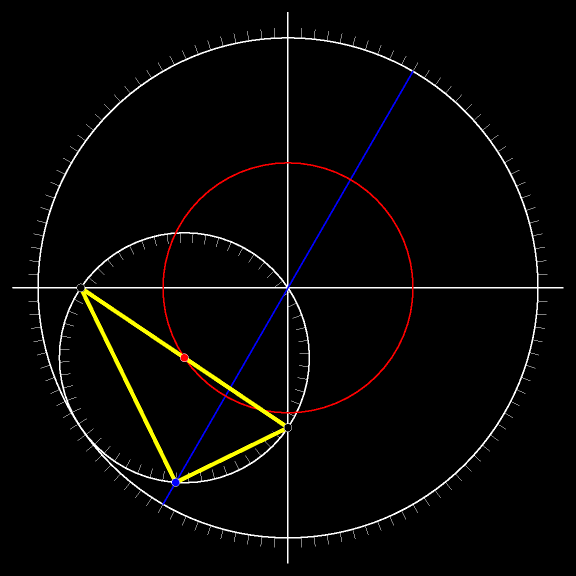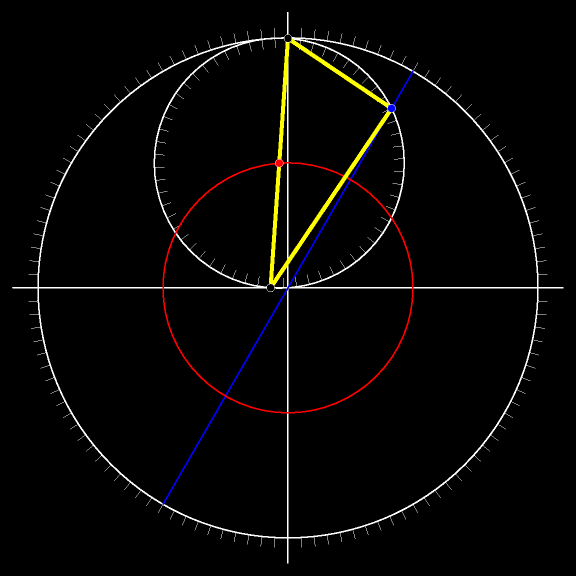Середина гипотенузы, как помните, движется по окружности, концентрической неподвижной окружности.

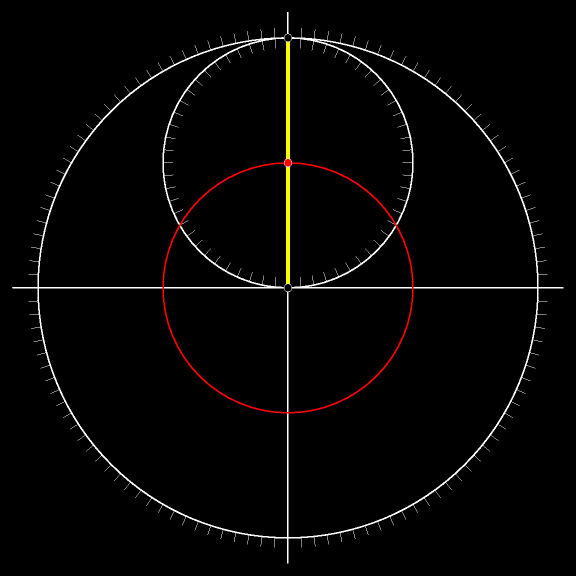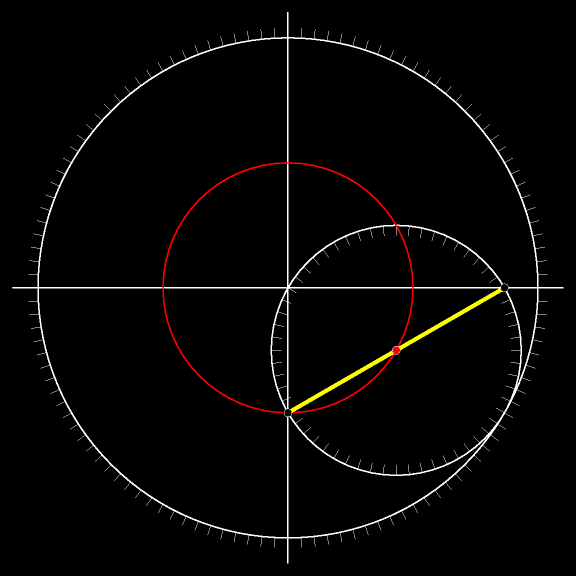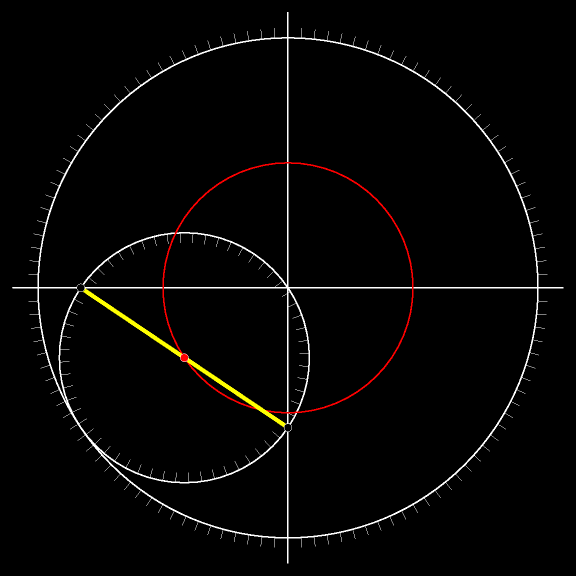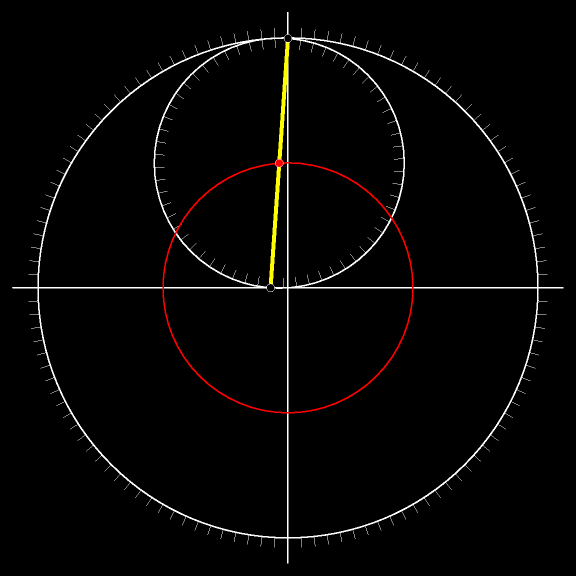Проследите взглядом за движением жёлтого отрезка — гипотенузы только что обсуждавшегося треугольника.

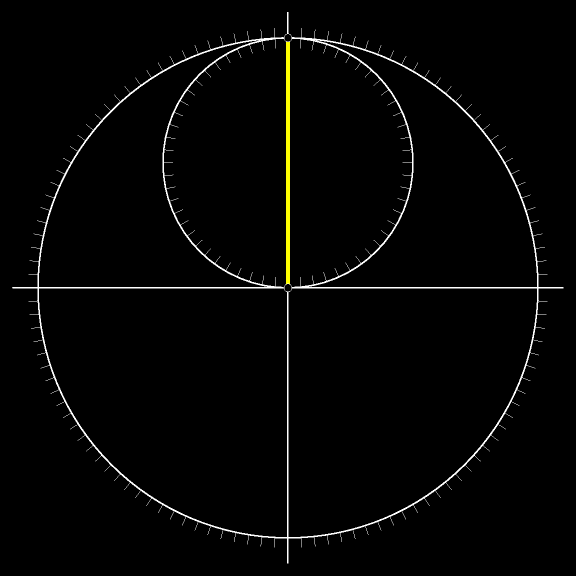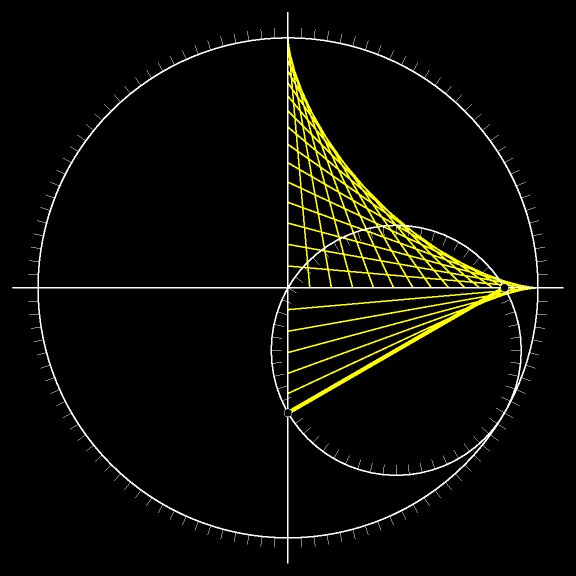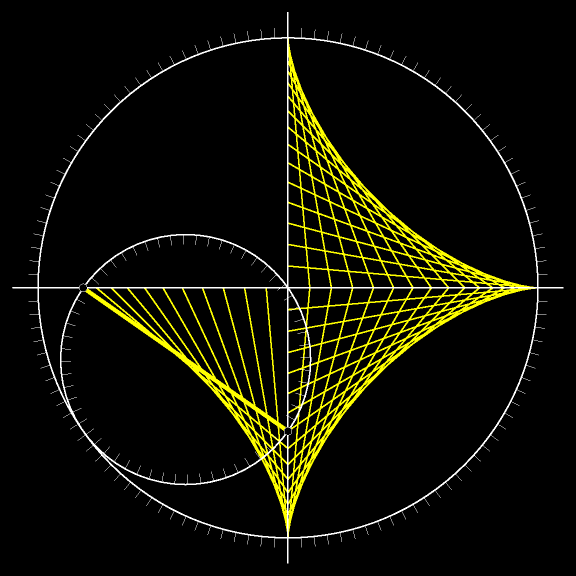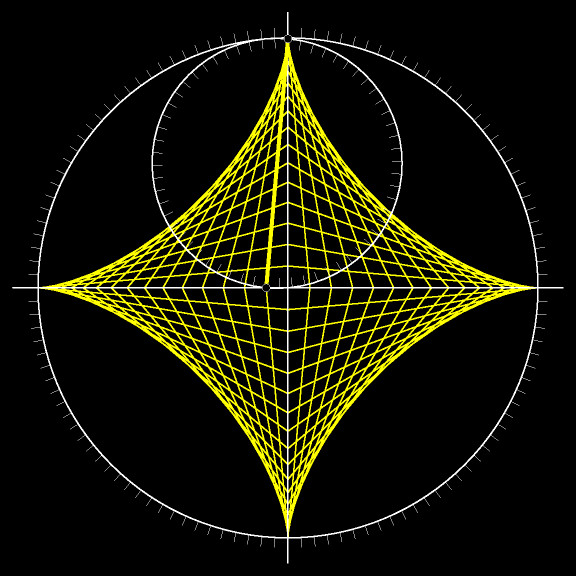Отрезок в каждый момент движения касается астроиды. А объединение всех возможных положений жёлтого отрезка — внутренность астроиды.

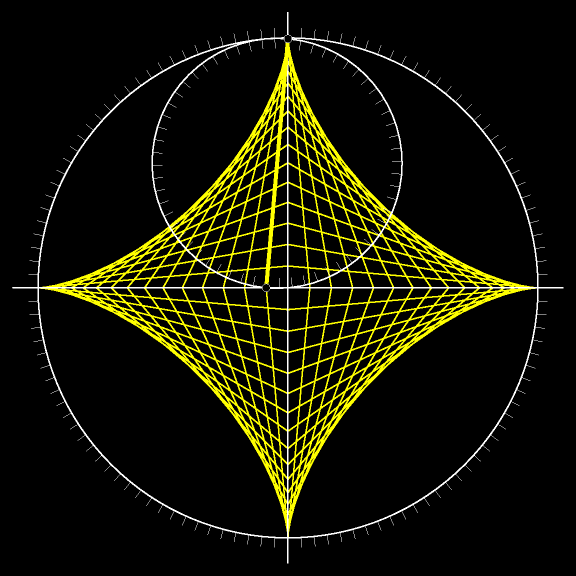На предыдущем рисунке отрезки двигались, а на следующем — один фиксированный момент из бесконечного множества.

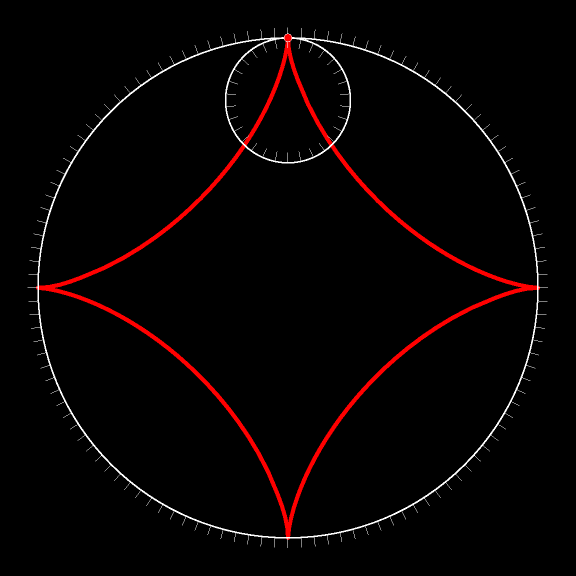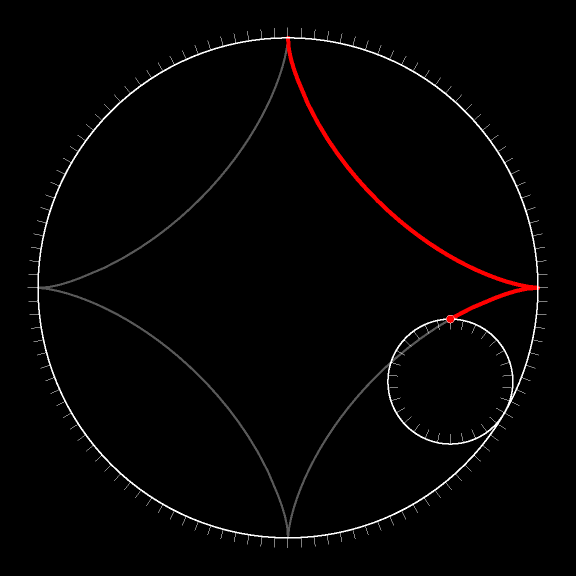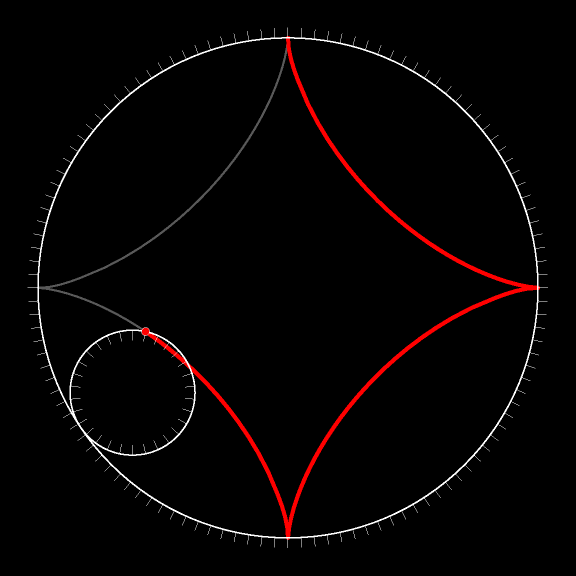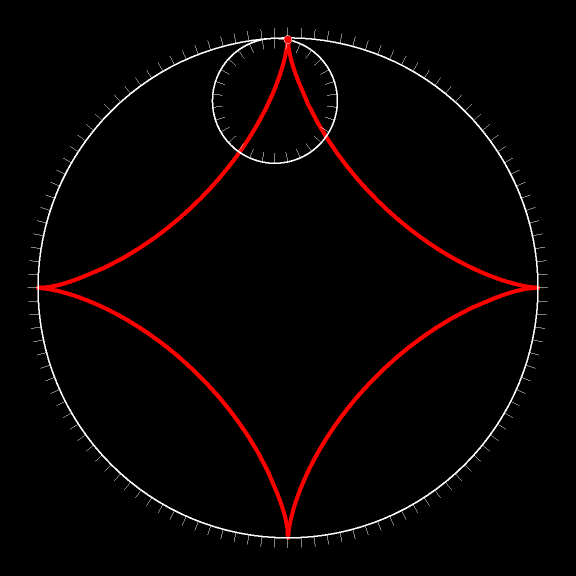
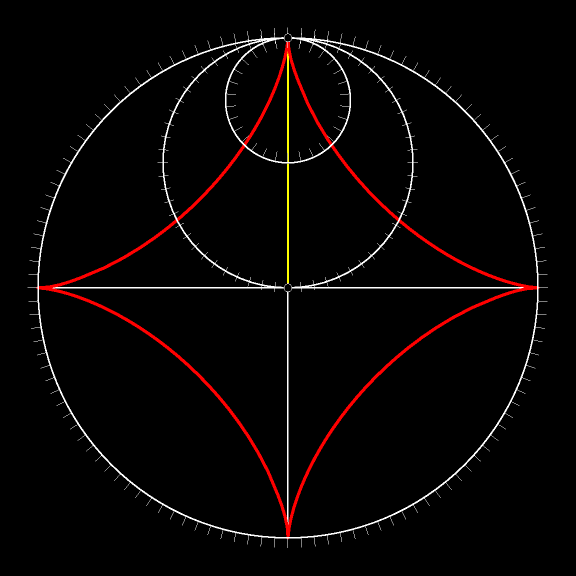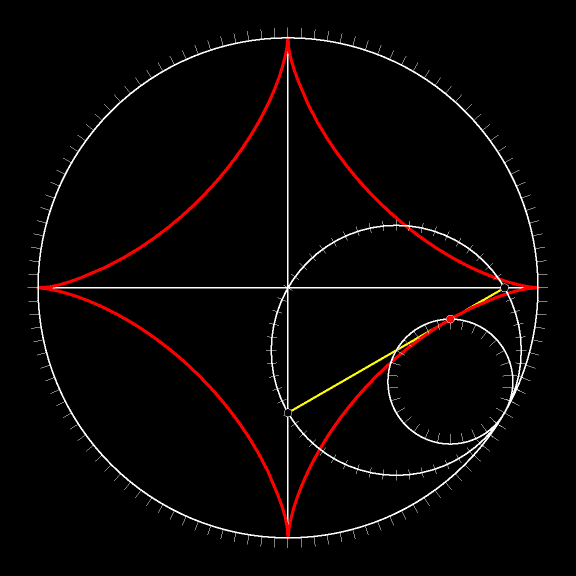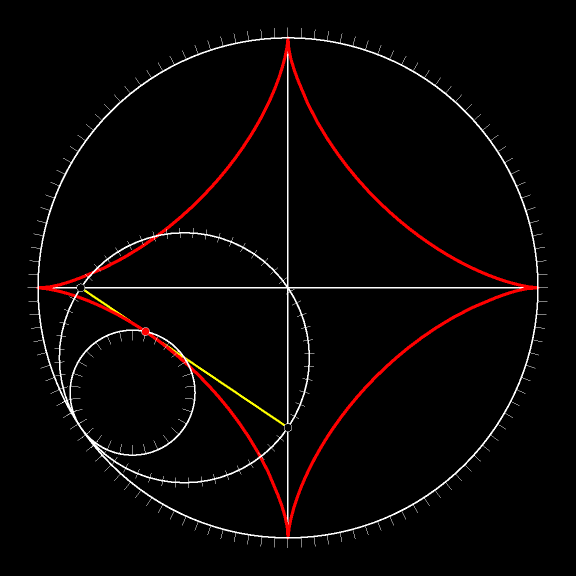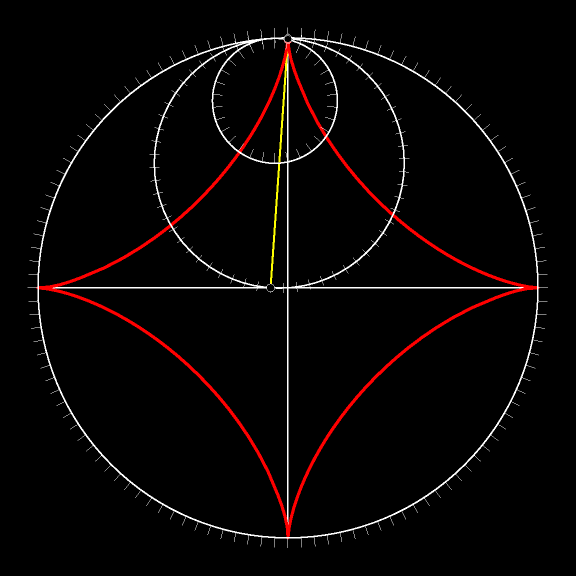
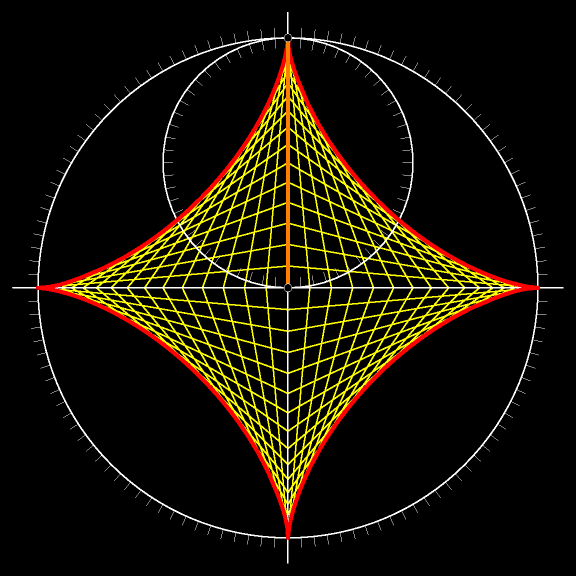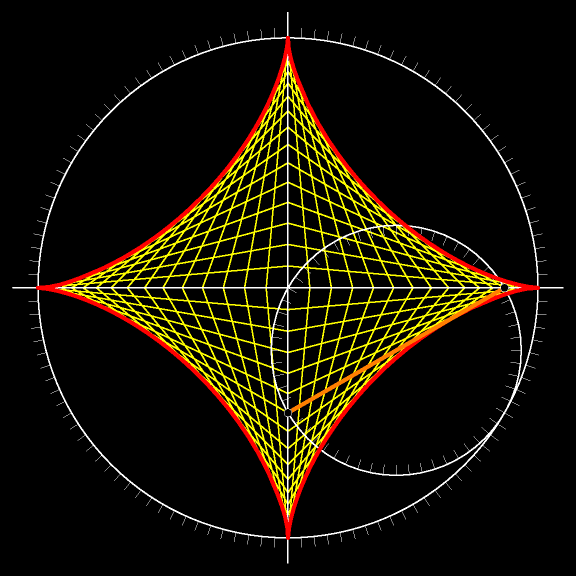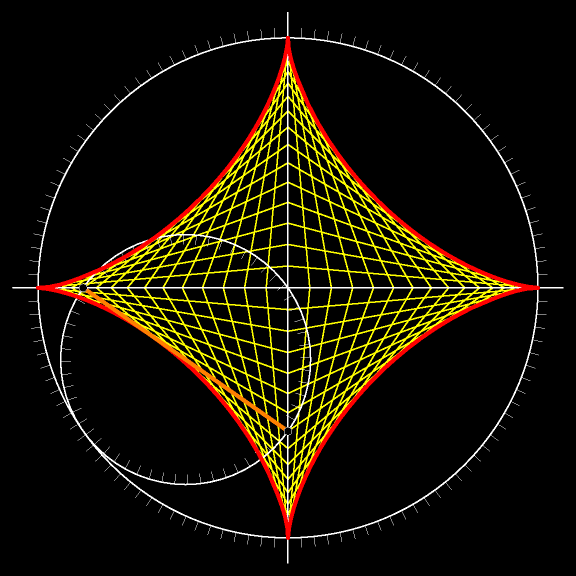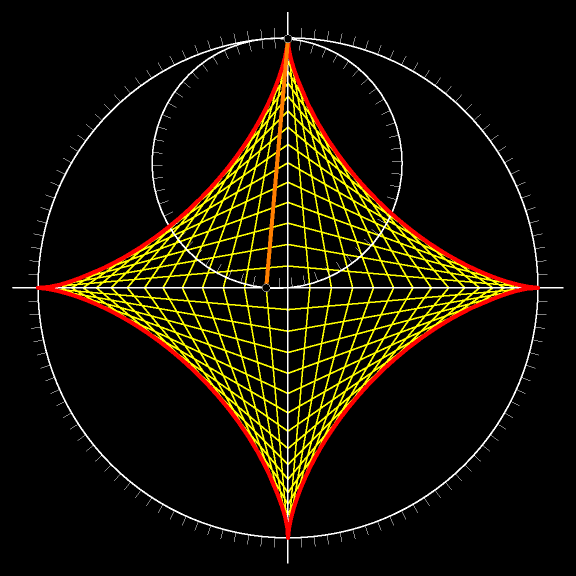А на следующем мультфильме астроида выделена красным цветом.

Рассмотрим окружность, радиус которой вчетверо меньше радиуса неподвижной окружности. Траектория движения точки такой окружности, когда она катится (без проскальзывания!) внутри подвижной окружности — та же самая астроида!

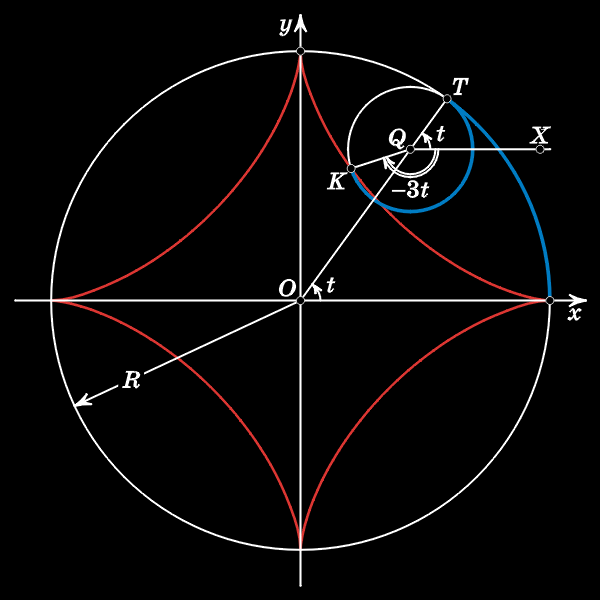Доказать равносильность двух определений астроиды можно при помощи метода координат и формул синуса и косинуса утроенного угла.

Доказать равносильность двух определений астроиды можно и без применения метода координат — при помощи идей механики. Смотрите, как катятся без проскальзывания две окружности и диаметр по гладкой — но не обязательно совершенно прямой — дороге.

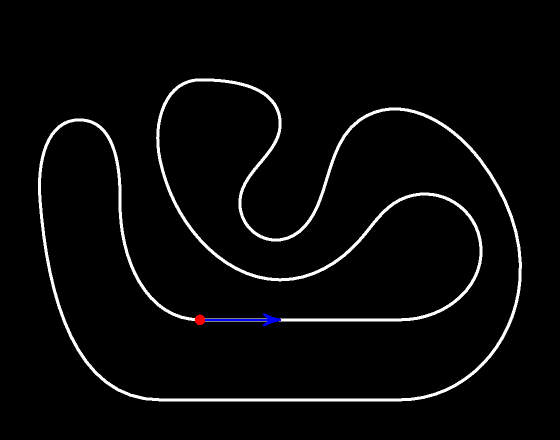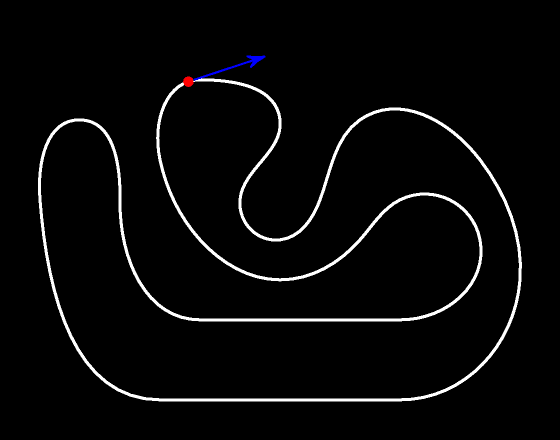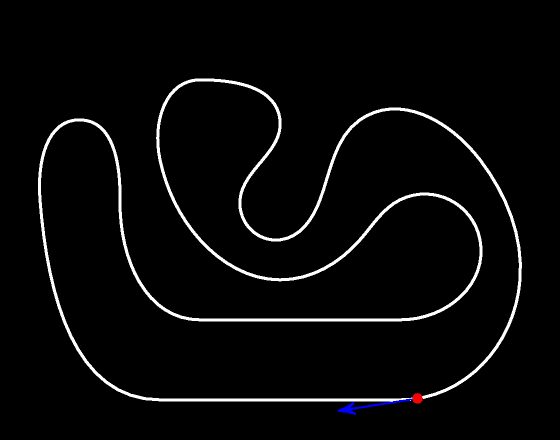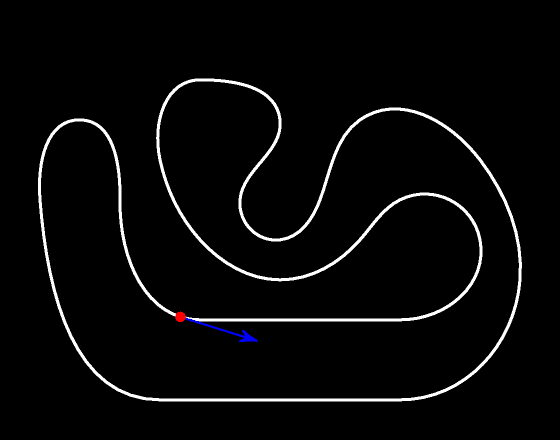При любом движении вектор скорости в любой момент времени касается траектории движения.

При поступательном движении векторы скоростей всех точек сонаправлены и равны по длине.

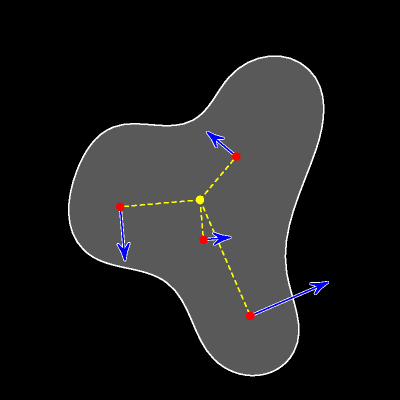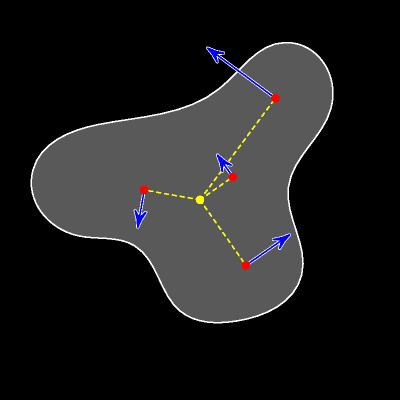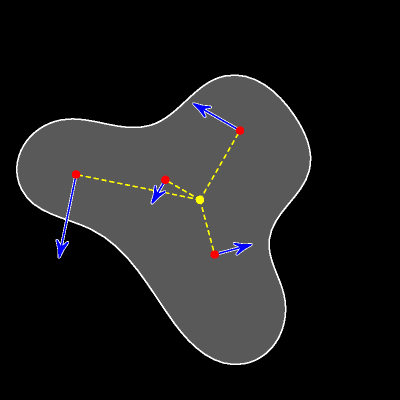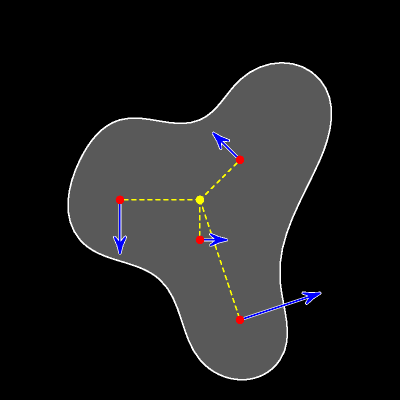При вращательном движении вектор скорости любой точки перпендикулярен радиус-вектору этой точки, а длина вектора прямо пропорциональна расстоянию от точки до центра вращения.

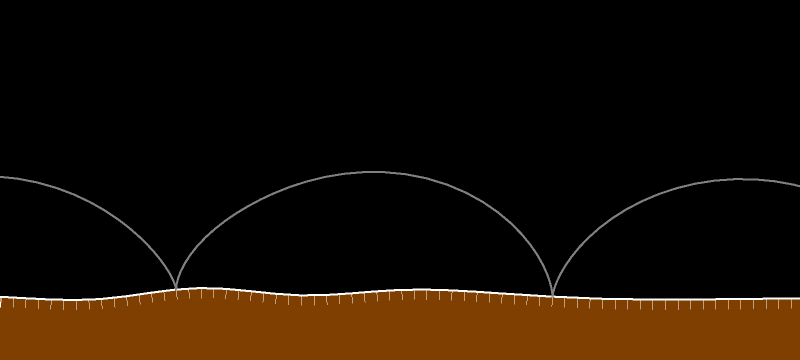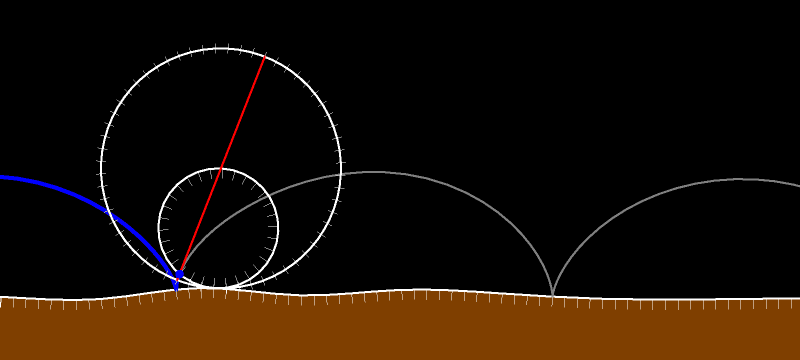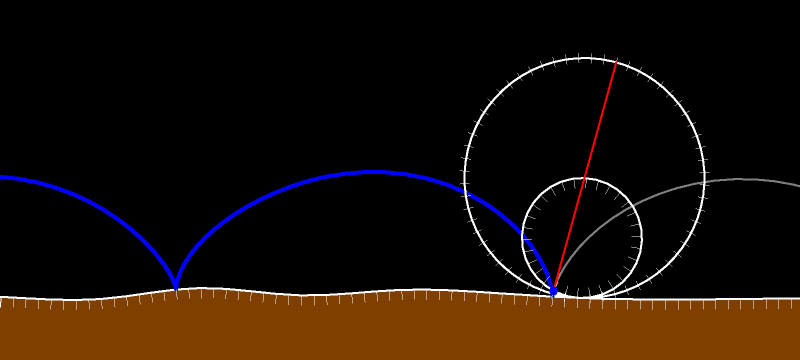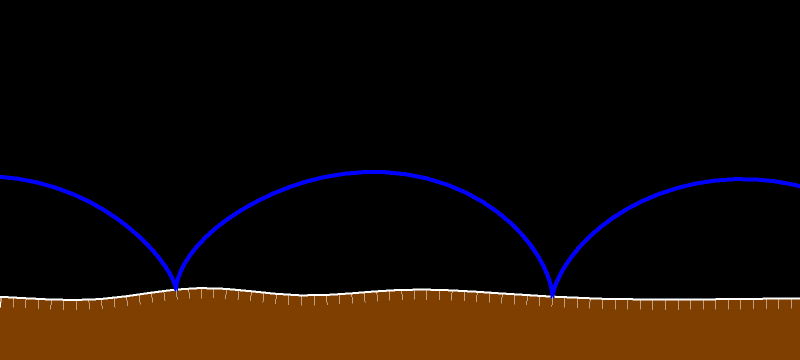
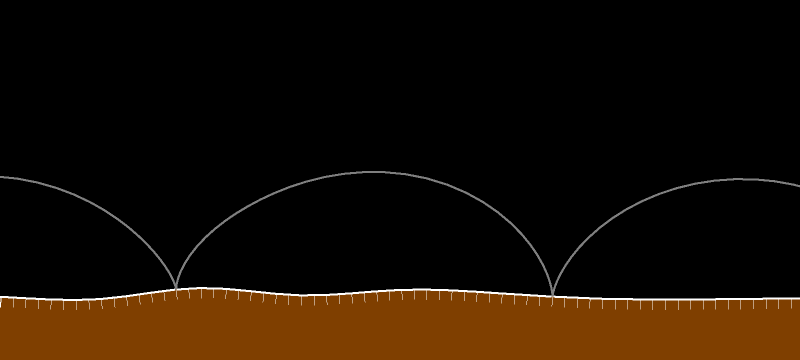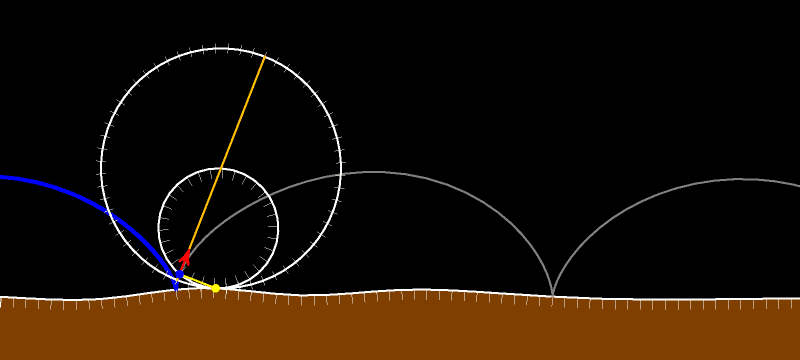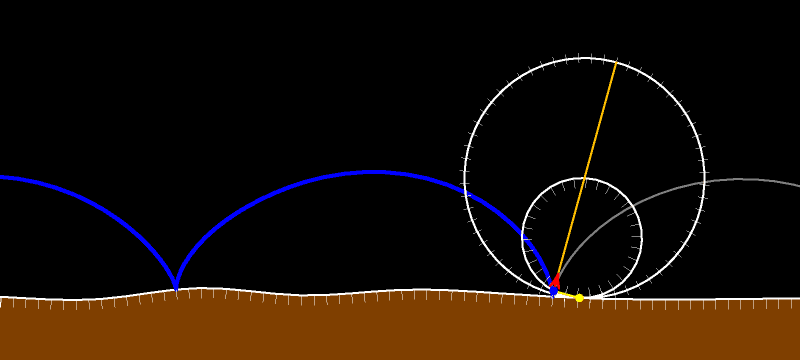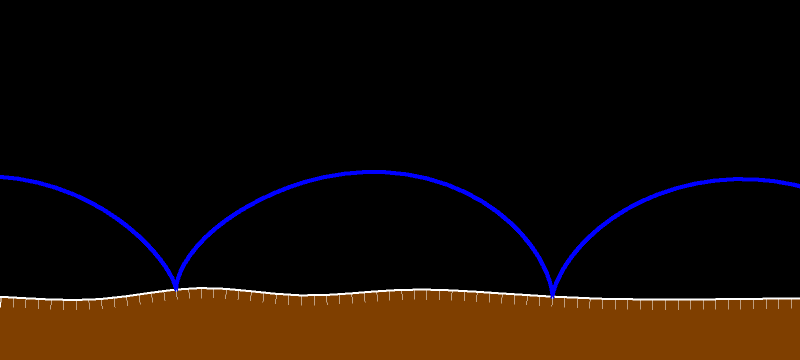
При движении без проскальзывания в каждый данный момент времени мгновенным центром вращения является точка касания катящегося тела с неподвижной дорогой. Это означает, что (красный) вектор скорости любой точки перпендикулярен отрезку, соединяющему рассматриваемую (синюю) точку с (жёлтой) точкой касания. А длина вектора скорости прямо пропорциональна расстоянию от точки до точки касания.

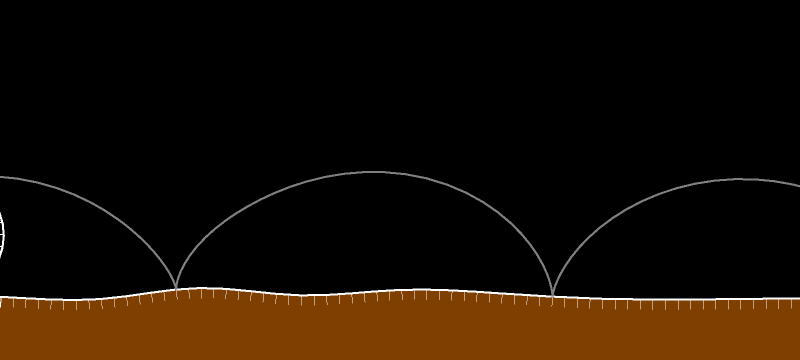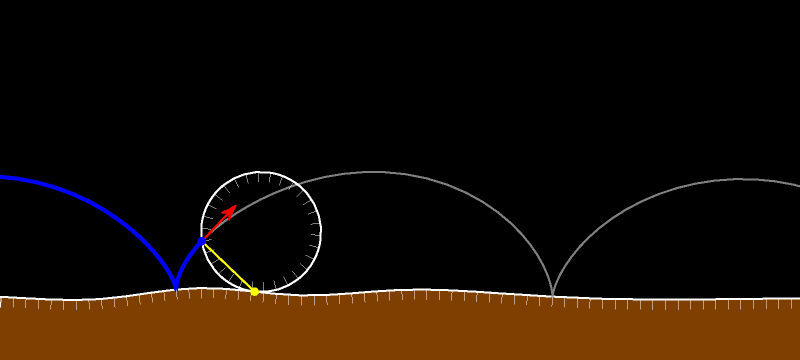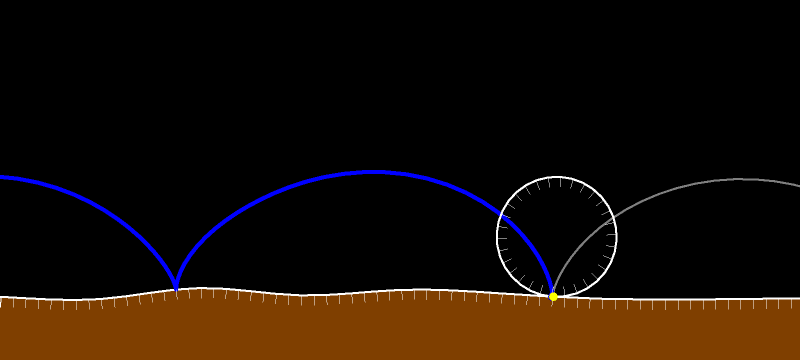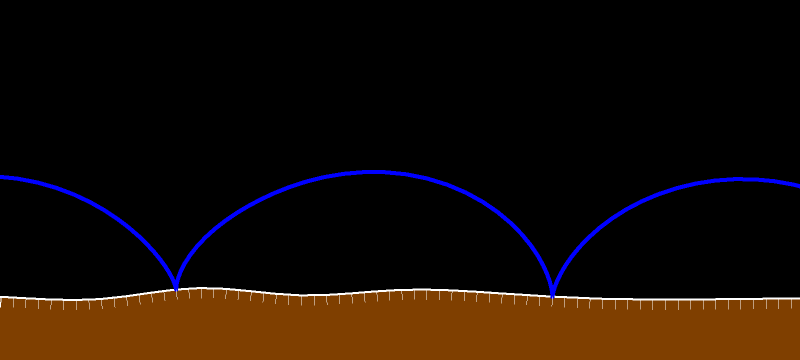
Вектор скорости касается траектории рассматриваемой нами точки. Он перпендикулярен жёлтому отрезку. Поскольку внутренняя окружность без проскальзывания движется по внешней, то рассматриваемая синяя точка в силу теоремы Торричелли движется по диаметру внешней окружности. Вектор скорости направлен вдоль диаметра.

Применяя только что сделанные наблюдения к случаю, когда дорога — окружность, радиус которой вдвое больше радиуса движущейся окружности и, соответственно, вчетверо больше радиуса внутренней движущейся окружности, мы доказываем равносильность двух определений астроиды!

Рассмотрим астроиду ещё с одной стороны. Пусть две полосы — вертикальная ширины a и горизонтальная ширины b — пересекаются под прямым углом.

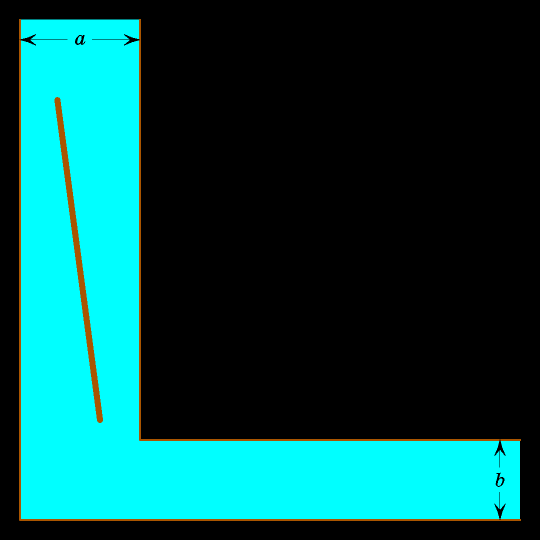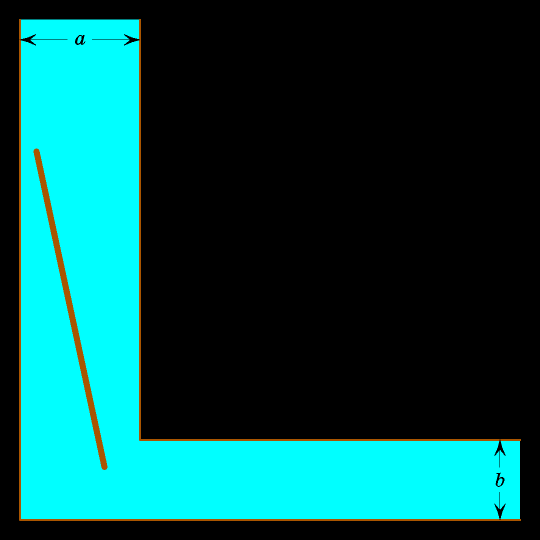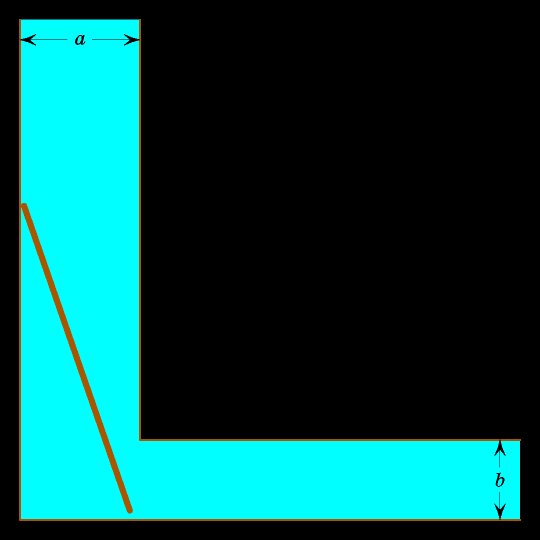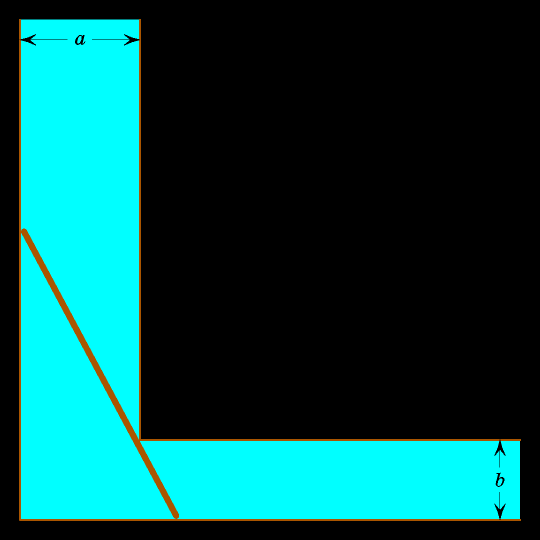
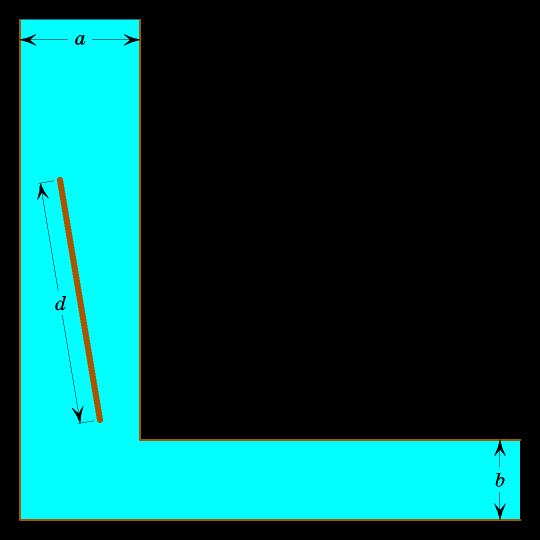Выясним, отрезки какой длины могут из вертикального положения в вертикальной полосе перейти в горизонтальное положение в горизонтальной полосе. Другими словами, сколь длинные брёвна могут пройти поворот?

Очевидно, если бревно не слишком длинное, то поворот возможен.

А если бревно слишком длинное, то оно обязательно застрянет.

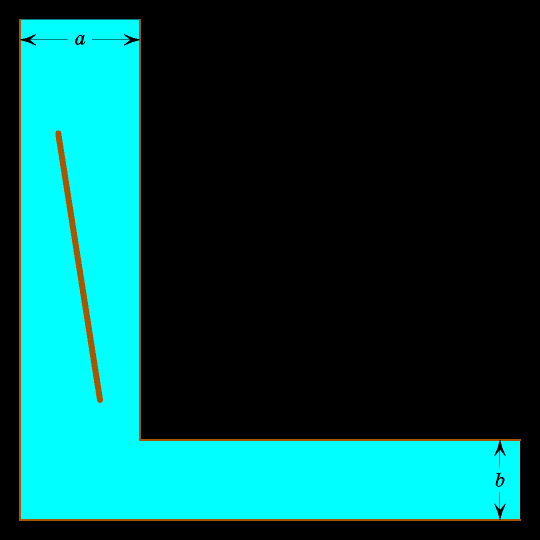Подумайте, как лучше всего двигать бревно? Очевидно, сначала его надо прижать к вертикальной левой прямой, затем поворачивать так, чтобы верхний конец упирался в вертикальную левую прямую, а нижний — в нижнюю горизонтальную прямую.

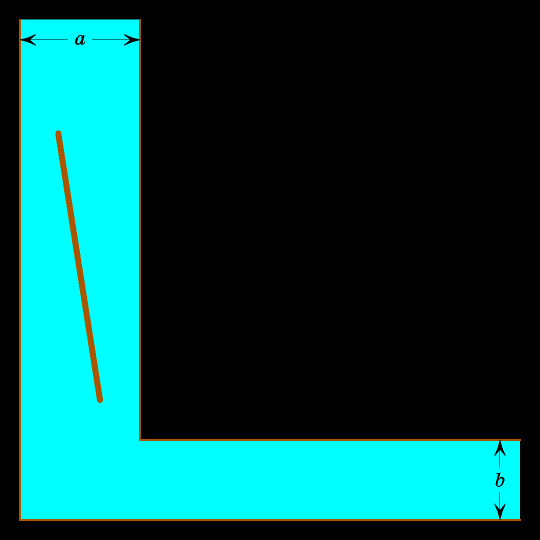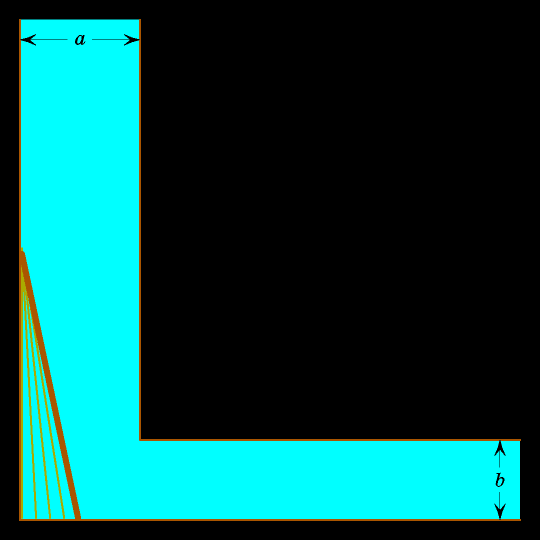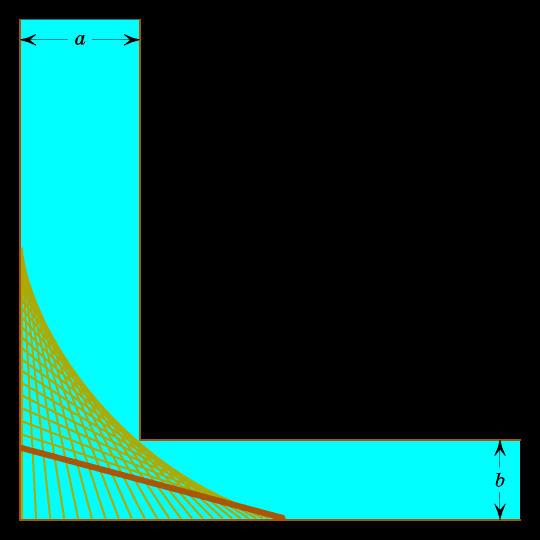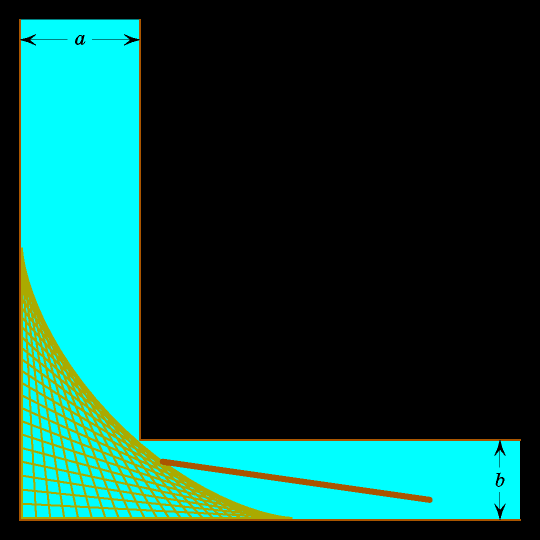При этом своём движении бревно заметает внутренность астроиды. Застрянет бревно или нет, зависит от того, внутри или вне астроиды лежит вершина угла, образованного правой вертикальной и верхней горизонтальной прямыми.

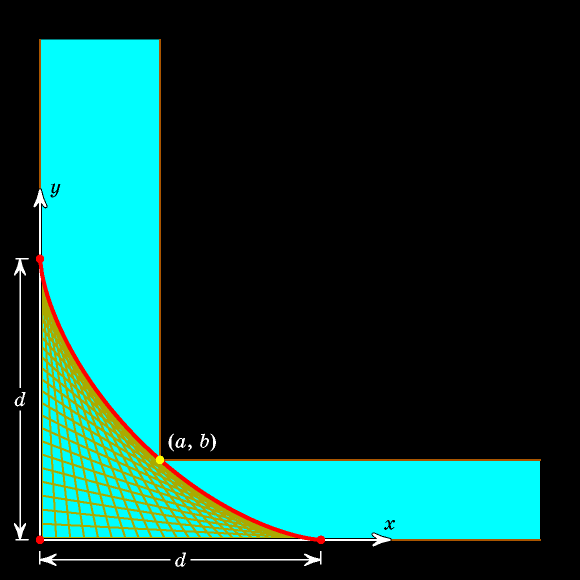В виде неравенства это записывается так: если сумма a^2/3 + b^2/3 больше величины d^2/3, то бревно сможет пройти поворот, а если меньше, то застрянет.