Конкурс имени А.П. Савина «Математика 6-8»
Задачи четвёртого номера 2000 года
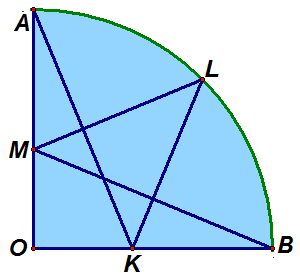 1. Криволинейный треугольник OAB представляет собой четверть круга. Из вершины A исходит луч, который, отразившись последовательно от радиуса OB в точке K, от дуги AB в точке L и от радиуса OA в точке M, попадает в вершину B. Докажите, что если L — середина дуги AB, то величины углов AKL, KLM и LMB равны 45°. 1. Криволинейный треугольник OAB представляет собой четверть круга. Из вершины A исходит луч, который, отразившись последовательно от радиуса OB в точке K, от дуги AB в точке L и от радиуса OA в точке M, попадает в вершину B. Докажите, что если L — середина дуги AB, то величины углов AKL, KLM и LMB равны 45°.
2. На доске мелом записаны целые числа от –10 до 10 включительно. Разрешено стереть любые два числа a и b, записав вместо них числа (3a – 4b)/5 и (4a + 3b)/5. Можно ли, произведя эту операцию несколько раз, добиться, чтобы все числа на доске стали равными?
3. Выпуклый четырёхугольник таков, что сумма расстояний от любой точки его внутренности до всех его сторон одна и та же для всех точек. Верно ли, что этот четырёхугольник — параллелограмм?
4. Может ли при каком-либо натуральном n число n2 + n + 1 быть квадратом целого числа?
5. Полицейские участки размещаются на перекрёстках города, причём для любого перекрёстка участок находится или на этом перекрёстке, или на соседнем. В городе 155 перекрестков; в каждом из них сходится не более шести улиц. Докажите, что в городе не менее 23 полицейских участков.
Задачи пятого номера 2000 года
6. Если сумма a + b двух положительных чисел a и b меньше удвоенной суммы 2(c + d) других двух положительных чисел c и d, то сумма квадратов первых двух чисел меньше увосьмерённой суммы квадратов третьего и четвёртого: a2 + b2 < 8(c2 + d2). Докажите это.
7. Четыре натуральных числа таковы, что произведение любых трёх из них является квадратом целого числа. Докажите, что каждое из четырёх чисел является квадратом целого числа.
8. Могут ли две биссектрисы внешних углов треугольника пересекаться на его описанной окружности?
9. Какое наибольшее количество ладей можно расставить на шахматной доске, чтобы каждая из них угрожала а) ни одной; б) одной; в) двум остальным?
10. Летом Маша отдыхала в молодёжном лагере, где вместе с ней находились 45 школьников. После окончания отдыха 950 пар обменялись адресами. Через некоторое время Маше понадобился адрес Ирины, с которой она адресом не обменялась. Докажите, что Маша может узнать адрес Ирины с помощью отдыхающих в лагере, то есть что существует цепочка из школьников, начинающаяся с Маши и оканчивающаяся Ириной, в которой каждая пара школьников обменялась адресами.
Задачи шестого номера 2000 года
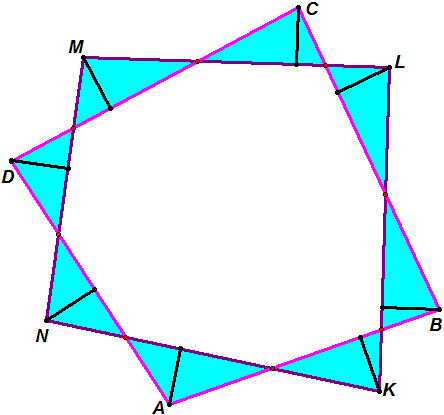 11. Два выпуклых четырёхугольника ABCD и KLMN расположены так, что в пересечении дают восьмиугольник. Все восемь высот в треугольниках, окаймляющих этот восьмиугольник, опущенные на его стороны, одинаковы. Докажите, что четырёхугольники имеют равные периметры и равные площади. 11. Два выпуклых четырёхугольника ABCD и KLMN расположены так, что в пересечении дают восьмиугольник. Все восемь высот в треугольниках, окаймляющих этот восьмиугольник, опущенные на его стороны, одинаковы. Докажите, что четырёхугольники имеют равные периметры и равные площади.
Указание
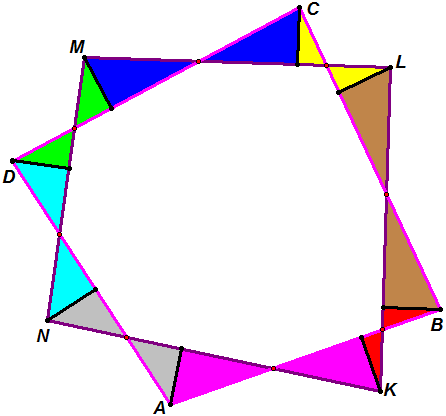
Указание. Одинаково окрашенные треугольники конгруэнтны:
Ответ. 59 259.
12. Имеется клетчатый бумажный квадрат со стороной 1111 клеток. Его требуется прямолинейными разрезами разделить на единичные квадратики, причём перед каждым очередным разрезом имеющиеся части разрешено как угодно перекладывать (не перегибая); за один приём можно резать сразу несколько частей. Какое наименьшее число разрезов требуется для разделения квадрата на единичные квадратики?
13. Нефтяная компания решила установить автозаправочные колонки на перекрёстках города, который имеет 162 отрезка улиц, соединяющих перекрёстки. Решено было устанавливать не более одной колонки на двух соседних перекрёстках. Известно, что в городе на каждом перекрёстке сходится не менее четырёх улиц. Докажите, что при этих условиях компания не сможет установить более 40 колонок.
14. а) Для любого натурального числа a существует такое натуральное число b,, что количество m цифр числа b больше количества n числа a, а сумма цифр произведения ab равна 9m. Докажите это.
б) Существуют 10 таких последовательных натуральных чисел, что сумма цифр первого из них равна 2000; сумма цифр второго равна 2001; ...; сумма цифр десятого равна 2009, причём каждое из этих чисел делится на сумму своих цифр. Докажите это.
15. Труляля и Траляля задумали по два натуральных числа. Сумма чисел, задуманных Труляля, равна произведению чисел, задуманных Траляля, а сумма чисел, задуманных Траляля, равна произведению чисел, задуманных Труляля. Какие числа могли задумать Труляля и Траляля?
Задачи первого номера 2001 года
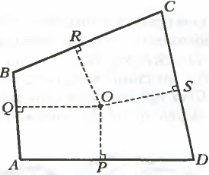 16. Внутри выпуклого четырёхугольника ABCD нашлась такая точка O, что основания перпендикуляров P, Q, R и S разбивают стороны четырехугольника на части, удовлетворяющие неравенствам DP ≥ PA, AQ ≥ QB, BR ≥ RC и CS ≥ SD. Докажите, что точка O — центр описанной около четырехугольника ABCD окружности. 16. Внутри выпуклого четырёхугольника ABCD нашлась такая точка O, что основания перпендикуляров P, Q, R и S разбивают стороны четырехугольника на части, удовлетворяющие неравенствам DP ≥ PA, AQ ≥ QB, BR ≥ RC и CS ≥ SD. Докажите, что точка O — центр описанной около четырехугольника ABCD окружности.
17. Существует ли такое натуральное число n, что последовательность чисел n + 1, 2n+ 1, Зn + 1, 4n + 1,... не содержит кубов?
18. Два жадных медвежонка нашли килограммовую головку сыра и попросили лису поделить её поровну. Лиса сначала разломила сыр на две неравные части, а затем откусила от одной из частей (не обязательно большей) половину. Так как части после этого всё-таки остались неравными, лиса снова откусила от одной из частей половину, и так далее. Лишь после десятого откусывания части сравнялись, но на долю медвежат досталось меньше 20 граммов сыра.
Обиженные медвежата потом жаловались, что части можно было бы уравнять, откусывая по половине от какой-либо части не больше трёх раз (а вовсе не десять!). Правы ли они?
19. В строку записано несколько чисел. Разрешено выбрать пару рядом стоящих чисел, в которой левое число больше правого, поменять оба числа местами и умножить оба на 2. Докажите, что рано или поздно перестановки прекратятся.
20. Начав с угла, пьяный король обошёл все клетки шахматной доски 5×5 по разу и вернулся на исходное поле, ни разу не сделав двух ходов подряд в одном направлении. Центры соседних полей его маршрута последовательно соединили отрезками. Докажите, что получилась самопересекающаяся ломаная.
| 
