«Квант» для «младших» школьников

Задачи первого номера 2007 года

1. Корабль считается попавшим в окружение, если он находится внутри выпуклого многоугольника, в вершинах которого располагаются корабли противника. Вы находитесь на капитанском мостике и в бинокль можете наблюдать все корабли противника. Как определить, попали вы в окружение или нет?

2. Существуют ли такие попарно неравные целые числа a, b, c, d, что a : b = c : d = (ac + 1) : (bd + 1)?

3. Гирьки массами 1, 2, 3, ..., n граммов, где n больше 6, разложили на две чашки весов так, что весы оказались в равновесии. Можно ли убрать с чашек три гирьки так, чтобы равновесие не нарушилось?

4. Почти прямоугольным называем треугольник, у которого есть угол, отличающийся от прямого не более чем на 15°. Почти равнобедренным называем треугольник, у которого есть два угла, отличающиеся не более чем на 15°. Верно ли, что любой остроугольный треугольник почти прямоугольный или почти равнобедренный?

5. По правилам регби, если игроку удалось прижать мяч к земле в специальной зачётной зоне (это называется попыткой), его команда получает 5 очков и, кроме того, игроку дают право пробить мячом по воротам, то есть выполнить реализацию. При попадании команда дополнительно зарабатывает 2 очка. Во время игры между командами «Рубильник» и «Дробильник» у команды «Рубильник» удачная реализация имела место в половине случаев, а у команды «Дробильник» — лишь в четверти всех случаев. Кто победил и с каким счётом, если обе команды в сумме набрали ровно 100 очков?

Задачи второго номера 2007 года

1. Три человека со стиральной машиной хотят переправиться через реку. Катер вмещает либо двух человек и стиральную машину, либо трёх человек. Беда в том, что стиральная машина тяжёлая, поэтому погрузить её в катер или вытащить из него можно только втроём. Смогут ли они переправиться?

2. «Cтарший военный врач Бауце из aabbb граждан выловил abccc симулянтов и поймал бы на удочку последнего, если бы этого счастливчика не хватил удар в тот самый момент, когда доктор на него заорал: «Кругом!»» В этом отрывке из «Похождений бравого солдата Швейка» мы заменили все цифры латинскими буквами (одинаковые — одинаковыми, разные — разными). Сколько симулянтов разоблачил бдительный доктор Бауце?

3. В 8А классе учатся 27 школьников. Им предложили посещать кружки по пению, свистению и чтению стихов. Каждый хочет посещать один или несколько из этих кружков. Оказалось, что в каждый кружок желает ходить более трети класса. Можно ли составить такие списки кружков, что во всех кружках будет поровну школьников и каждый будет ходить ровно в один из кружков, причём этот кружок будет одним из тех, куда он хотел ходить?

4. Щит короля Артура имеет форму восьмиугольника, который образовался из квадрата после отрезания одинаковых равнобедренных треугольников. Красный цвет, символ мужества, занимает на щите ту же площадь, что и синий — символ справедливости. Докажите это, не прибегая к вычислениям.

5. Таблицу 3×3 называют магическим квадратом, если все числа в ней различны, а суммы чисел во всех строках, во всех столбцах, а также в диагоналях одинаковы (например, как показано на рисунке). Существует ли магический квадрат, заполненный числами, обратными натуральным?

Задачи третьего номера 2007 года

1. Профессор заподозрил, что некоторые студенты спят на его лекции. Чтобы установить число безобразников, он незадолго до начала лекции скрытно установил храпометры во всех углах аудитории, представляющей собой правильный шестиугольник с длиной стороны a. Каждый храпометр улавливает количество спящих на расстоянии, не превышающем а. После лекции оказалось, что все храпометры в сумме зафиксировали 7 спящих. Сколько студентов спало на лекции?

2. Диагонали разрезали четырёхугольник на треугольники, которые попеременно окрашены в красный и синий цвета. Сумма площадей красных треугольников равна сумме площадей синих. Докажите, что хотя бы одна из диагоналей четырёхугольника делит его площадь пополам.

3. Любое ли натуральное число, делящееся на 9, отличается от некоторого натурального числа n на сумму цифр этого числа n?

4. Однажды физик, купив сахар и колбасу, решил проверить их вес на чашечных весах, случайно обнаруженных в магазине. Сахар на левой чашке весов он уравновесил гирей 8 кг на правой чашке, а колбасу на правой чашке уравновесил гирей 2 кг на левой чашке. Каково же было его удивление, когда, придя домой и проверив вес каждого товара на высокоточных электронных весах, он обнаружил, что общий вес его покупки больше 10 килограммов. Колбаса оказалась тяжелее сахара. «Ага, весы были неравноплечные!» — решил физик. Сколько в таком случае весят колбаса и сахар, если вес каждого товара выражается целым количеством килограммов?

5. В отчете Французской Академии наук за 1733 год среди прочих результатов и достижений указано, что когда некое тело подносится близко к лицу, оно «вызывает такие же ощущения, как если бы натолкнуться на невидимую паутину». О каком физическом эффекте идёт здесь речь?

Задачи четвёртого номера 2007 года

1. Обозначим П(n) произведение цифр десятичной записи натурального числа n, причём если число n само является цифрой, то П(n) = n. Например: П(5) = 5, П(25) = 10. Последовательно записаны такие числа: 1 + П(1), 2 + П(2), 3 + П(3),... Могут ли в этой последовательности 2007 подряд идущих чисел оказаться последовательными натуральными числами?

2. На острове проживают аборигены, каждый из которых либо всегда говорит правду, либо всегда лжёт. Как-то встретились три аборигена: Ах, Ох и Ух. Один из них сказал: «Ах и Ох — оба лжецы», другой сказал: «Ах и Ух — оба лжецы» (но кто именно что сказал, неизвестно). Сколько всего лжецов среди этих трёх аборигенов?

3. Может ли среднее арифметическое десяти различных натуральных чисел быть равно их наибольшему общему делителю?

4. Петя на каждом листе тетради из 96 листов нарисовал веселую рожицу (в анфас) либо с одной, либо с другой стороны листа, так что если положить закрытую тетрадь на стол, то некоторые рожицы будут «смотреть» на него, а остальные — от него. Верно ли, что можно раскрыть тетрадь (или вообще не раскрывать) в таком месте, чтобы на Петю и от него «смотрело» одинаковое количество рожиц?

5. Правильный восьмиугольник разрезан на части, которые закрашены в четыре цвета. Докажите, что каждым цветом закрашена одна и та же площадь.

Задачи пятого номера 2007 года

1. В Солнечном городе образованы три партии коротышек: винтиков, шпунтиков и болтиков. Для любых трёх коротышек есть партия, в которую входят по крайней мере двое из них. Верно ли, что все члены одной из партий являются членами какой-то из двух других партий?

2. Для любых неотрицательных чисел a и b докажите, что число (a² + b²)³ не меньше числа (a³ + b³)².

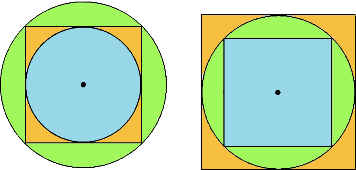3. В круг площади 1 вписали квадрат, а в него — новый круг, который закрасили в синий цвет. Затем в квадрат площади 1 вписали круг, а в него — квадрат, который закрасили в синий цвет. Чья площадь больше: синего круга или синего квадрата?

4. Колонна солдат-новобранцев выстроилась несколькими одинаковыми шеренгами, составляющими прямоугольник. По команде «смирно» некоторые из солдат с перепугу сделали поворот направо, некоторые — налево, другие — кругом, а кое-кто вообще остолбенел и остался неподвижен. Далее через каждую секунду происходит следующее: каждый новобранец, оказавшийся лицом к лицу с другим солдатом, делает поворот направо. а) Докажите, что рано или поздно такие повороты прекратятся. б) Прекратятся ли повороты, если поворачиваются не оба солдата, оказавшиеся лицом к лицу, а только один из них?

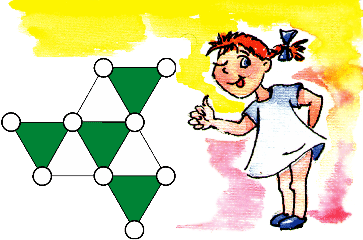5. Числа от 1 до 9 расставьте в кружки фигуры так, чтобы сумма трёх чисел, расположенных в кружках–вершинах всех белых треугольников, была одной и той же, а во всех зелёных — тоже одной и той же, но на 3 больше.

Задачи шестого номера 2007 года

1. (a – b + 2007), (b – c + 2007) и (c – a + 2007) — последовательные целые числа. Какие?

2. Сумма двух натуральных чисел равна 2007. Какое наибольшее значение может иметь остаток от деления большего числа на меньшее? Тот же вопрос, если сумма равна 2008.

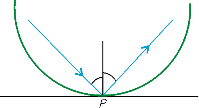3. Бильярдный шарик, двигаясь без трения на круглом бильярдном столе без луз, отражается от точки Р борта и через 5 секунд отражается второй раз в той же самой точке Р (возможно, в другом направлении, чем в первый раз). Отражение шарика от борта происходит по закону: «угол падения равен углу отражения». Докажите, что движение шарика периодично с периодом 5 секунд.

4. Белые шахматные фигуры (полный комплект: восемь пешек, две ладьи и так далее) перессорились и решили друг друга побить. Расставьте их (только их!) на шахматной доске так, чтобы никакая фигура никакую не била.

Предупреждение   I способ   II способ   III способ   IV способ   Способы I–IV

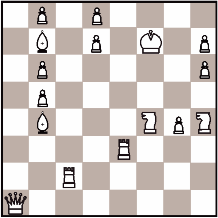Предупреждение. Показанное на диаграмме решение не годится, поскольку пешки не могут стоять на восьмой горизонтали.

I способ. Ферзь a8, ладьи f6, g1, слоны d2, h3, кони c2, h4, король c5, пешки b2, b3, c7, e2, e7, h2, h5 и h7.

II способ. Ферзь g1, ладьи f7, h6, слоны c8, d8, кони a8, b8, король a2, пешки a4, b4, c2, c4, d2, e2, e4 и e5.

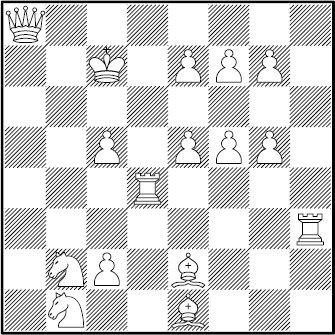III способ. Ферзь a8, ладьи d4, h3, слоны e1, e2, кони b1, b2, король c7, пешки c2, c5, e5, e7, f5, f7, g5 и g7.

IV способ. Ферзь c8, ладьи e7, g6, слоны d4, h2, кони a1, h1, король f3, пешки a2, a3, a5, d2, d3, d4, d5 и h4.

5. Математик C предложил математикам А и В такую загадку.
— Я задумал три попарно различных натуральных числа, произведение которых не превосходит 50. Сейчас я по секрету сообщу А это произведение, а В — сумму задуманных чисел. Попробуйте отгадать эти числа.
Узнав произведение и сумму, соответственно, А и В вступили в диалог.
А: Я не знаю этих чисел.
В: Если бы мое число было произведением, я бы знал загаданные числа.
А: Но я все равно не знаю этих чисел.
В: Да и я не знаю.
А: А я уже знаю их.
В: Да и я знаю.
Что это за числа?