«Квант» для «младших» школьников

Задачи первого номера 2003 года

1. У завхоза Васи было трое одинаковых чашечных весов. В одних потерялась часть деталей, и теперь они могут показывать что угодно. Любые весы помещаются на одну чашу других весов. За какое наименьшее количество взвешиваний можно определить неисправные весы?

Ответ   Указание   Решение

2. Равносторонний треугольник как-то разрезан на равносторонние треугольники, периметр каждого из которых — целое число. Докажите, что периметр исходного треугольника — целое число.

3. Архипелаг состоит из 7 островов, расположенных вблизи материка. С каждого острова выходит 3 моста. Между любыми двумя островами, а также между каждым островом и материком имеется не более одного моста. С острова Чунга на остров Чанга переехать нельзя. Сколько мостов связывают острова архипелага с материком?

4. Два квадрата 10×10 одинаково раскрашены в 3 цвета, причём никакие две соседние по стороне клетки не покрашены в один цвет. Каждый квадрат разрезали произвольным образом на прямоугольники 2×1. Из частей одного квадрата составили новый квадрат 10×10. Всегда ли из частей второго квадрата можно составить такой же квадрат, как из первого?

5. Вставьте вместо многоточий числа (в десятичной записи) так, чтобы было верным утверждение:
«В этом предложении цифра 0 встречается ... раз(а);
цифры, не превышающие 1, — ... раз(а);
цифры, не превышающие 2, — ... раз(а);
цифры, не превышающие 3, — ... раз(а);
цифры, не превышающие 4, — ... раз(а);
цифры, не превышающие 5, — ... раз(а);
цифры, не превышающие б, — ... раз(а);
цифры, не превышающие 7, — ... раз(а);
цифры, не превышающие 8, — ... раз(а);
цифры, не превышающие 9, — ... раз(а)».

Задачи второго номера 2003 года

1. Любые четыре из некоторых десяти гирек перевешивают любые три другие из этих гирек. Верно ли, что любые три из этих десяти гирек перевешивают любые две другие?

2. В клубе встретились 20 джентльменов. Некоторые были в шляпах, а некоторые — нет. Время от времени один из джентльменов снимал с себя шляпу и надевал её на одного из тех, у кого в этот момент шляпы не было. В конце 10 джентльменов подсчитали, что каждый из них отдавал шляпу большее число раз, чем получал. Сколько джентльменов пришли в шляпах?

3. В Ачухонии жили 100 рыцарей, 99 принцесс и 101 дракон. Рыцари убивают драконов, драконы едят принцесс, а принцессы изводят до смерти рыцарей. Древнее заклятие запрещает убивать того, кто сам погубил нечётное число других жителей. Сейчас в Ачухонии остался всего один житель. Кто это?

4. В нескольких кошельках лежат одинаковые суммы денег. Если в каждый кошелёк добавить по копейке, а количество кошельков уменьшить на 1%, общая сумма денег уменьшится. Если, наоборот, из каждого кошелька забрать по копейке, а количество кошельков увеличить на 1%, общая сумма денег опять-таки уменьшится. Во сколько раз увеличится общая сумма, если количество кошельков не менять, но в каждый кошелёк добавить по рублю?

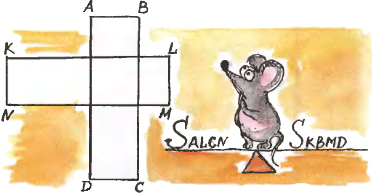5. Прямоугольники ABCD и KLMN имеют соответственно параллельные стороны и расположены так, как показано на рисунке. Докажите равенство площадей четырёхугольников ALCN и KBMD.

Задачи третьего номера 2003 года

1. В некотором государстве живут только правдуны (которые говорят только правду) и лгуны (которые всегда лгут). В течение одного вечера в дом вошли 10 человек, и каждый из них (кроме последнего) записал на специальном листе бумаги, кто вошёл в дом после него — правдун или лгун. Если верить всем записям, то в дом входили только лгуны. Сколько лгунов пришло в дом на самом деле?

2. На большом прямоугольном столе лежат линейка и кирпич, имеющий форму прямоугольного параллелепипеда. Как измерить диагональ кирпича, не пользуясь ничем, кроме перечисленного, и приложив линейку только один раз?

3. Расстояние от Гадюкина до Мартышкина не менее 9 км. На расстоянии не менее 1 км и не более 3 км от Гадюкина растёт берёза, а на расстоянии не менее 5 км и не более 7 км от Гадюкина растёт дуб. Точно посередине между березой и дубом зарыт клад, причём это место находится не дальше 4 км от Мартышкина. На каком расстоянии от Гадюкина зарыт клад?

4. Из трёх цифр x, y, z составлены три десятичные периодические дроби x,(yz), y,(zx) и z,(xy) таким образом, что выполнено равенство

x,(yz) + y,(zx) = z,(xy).

Докажите, что среди цифр x, y и z имеются одинаковые.

5. Шулер Фукс выкладывает в один ряд лицом вниз три карты: даму, короля и туза, не соблюдая порядок старшинства (туз старше короля, а король старше дамы). Моряк Лом должен переложить их по старшинству слева направо. Перед каждой попыткой он может указать на любые две карты и узнать, какая старше. Если после этого он выложит карты правильно, то Фукс об этом сообщает. Если нет, то Лом отворачивается, а Фукс в это время меняет две рядом лежащие карты. Есть ли у Лома способ справиться с заданием не более чем за три попытки?

Задачи четвёртого номера 2003 года

1. Вася и Петя задумали по три числа. Каждое из васиных чисел умножили на каждое из петиных чисел и результаты записали в таблицу. Вовочка стёр некоторые из чисел этой таблицы. Восстановите стёртые числа.

2. Чему равно натуральное число n, если известно, что цифровой ребус ЖУК · n = ЖУКИ имеет решение? (Одинаковым буквам русского алфавита соответствуют одинаковые цифры, разным буквам — разные.)

3. Имеются 25 одинаковых картонных квадратов, около вершин которых одинаково записаны по часовой стрелке числа 0, 1, 4, 3. Все квадраты сложили в стопку. Могли ли все четыре суммы чисел, записанных около вершины стопки, быть одинаковыми?

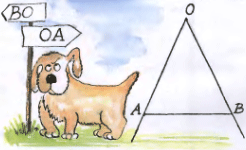4. Две прямолинейные аллеи парка пересекаются в его центре — точке A. На равном удалении от центра — в точках A и B — находятся две скамейки, тоже соединённые аллеей. На каждой скамейке сидит девочка, а собака Моська располагается ровно посередине между ними. Девочки одновременно встали и с одинаковой скоростью пошли по аллеям. Одна из них пошла по аллее OA от центра, а другая — по аллее BO к центру парка. Собака в каждый момент времени занимает середину отрезка, соединяющего двух девочек. Выбежит ли собака Моська за пределы аллеи AB, пока одна из девочек будет двигаться к центру парка?

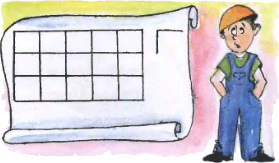5. В мастерской изготавливают прямоугольные решетки, состоящие из квадратных ячеек со стороной 1. Для этого используют заготовки, состоящие из двух стержней длиной 1, сваренных под прямым углом в виде буквы «Г». При изготовлении решётки запрещено накладывать стержни друг на друга; допускается лишь сваривать их между собой в точках касания. Для каких m и n мастерская может изготовить решетку размером m×n?

Задачи пятого номера 2003 года

1. Профессор Мумбум-Плюмбум пытается подобрать две цифры a и b такие, что обыкновенная дробь a/b равна десятичной дроби a,b. Удастся ли ему это сделать?

2. Стал я рядом с цифрой пять
Слева двойки выставлять.
Двойку выставил — и рад:
Получается квадрат. (25 = 5²)
Снова двойка — снова рад:
У меня опять квадрат. (225 = 15²)
Стал я дальше выставлять, (2225, 22225, 222225,...)
А квадратов — не видать.
Помогите разобраться.
Вдруг не стоит и стараться?

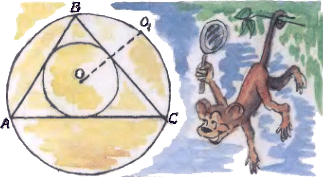3. В треугольнике ABC центр вписанной окружности отразили симметрично относительно стороны BC — получили точку, лежащую на описанной окружности. Докажите, что величина угла A равна 60°.

4. На станцию Нью-Васюки прибыл товарный поезд, на каждом вагоне которого написан восьмизначный номер. Этот номер может начинаться с нуля, но не может состоять из одних нулей. В номере головного вагона каждая содержащаяся в нём цифра встречается одинаковое количество раз. Номер хвостового вагона обладает тем же свойством. Какие это номера, если номер головного вагона равен квадрату номера хвостового вагона?

5. Андрей взял клетчатую бумагу 10×10 и во всех клетках как попало провёл по одной диагонали. После чего 200 полученных треугольников раскрасил в красный, жёлтый и синий цвета так, что любые два треугольника, имеющие общую сторону, оказались окрашенными в разные цвета. Считаете ли вы, что Андрею повезло, или трёх цветов всегда достаточно?

Задачи шестого номера 2003 года

1. На шахматной доске стоят фигуры. Когда Аня подсчитала количества фигур, стоящих на каждой из вертикалей, у неё все числа получились разными. Андрей подсчитал количества фигур, стоящих на каждой из горизонталей. Могло ли ни одно из чисел, полученных Андреем, не совпасть ни с одним из чисел, полученных Аней?

2. Произведение пяти чисел не равно нулю. Каждое из этих чисел уменьшили на единицу, при этом произведение не изменилось. Приведите пример таких чисел.

3. Сумма величин углов A, B и C выпуклого шестиугольника ABCDEF равна сумме величин углов D, E и F. Докажите, что у шестиугольника есть две противоположные стороны.

4. Прокрустик полагает, что из любого неравнобедренного треугольника можно получить прямоугольный треугольник, увеличив все его стороны на одну и ту же величину, либо уменьшив все его стороны на одну и ту же величину. Прав ли Прокрустик?

5. На съезд партии умеренного прогресса собрались 100 делегатов, каждый из которых либо всегда говорит правду, либо всегда лжёт. Первое же заседание по одному покинули 60 делегатов, каждый из которых после выхода из зала объявил журналистам: «Лжецов cреди оставшихся там больше, чем правдивых». Сколько всего лжецов среди делегатов съезда?