«Квант» для «младших» школьников
Задачи первого номера 1982 года
 1. Толя и Саша, сыграв партию в домино, выложили все косточки. У них получилась прямоугольная рамка. Очки заменены в этой рамке буквами (пустые клетки — это «нулевые» очки). На рисунке показано, как расположены косточки в вершинах рамки (они закрашены). Положения остальных косточек неизвестны, но известно, что суммы очков по горизонтальным и вертикальным сторонам рамки все одинаковы. Восстановите расположение косточек.
2. В 1982 году квадрат возраста Матлеба совпал с числом, образованным первыми тремя цифрами его года рождения. В каком году родился Матлеб?
3. В 1981 году 1 января и 31 декабря были одним и тем же днем недели. Будет ли так в 1982 году? И вообще, в какие годы 1 января — тот же день недели, что и 31 декабря?
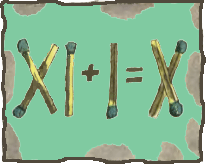 4. На листке бумаги из спичек выложили равенство XI + I = X (знаки действия — не из спичек). Какое минимальное количество спичек нужно переложить, чтобы равенство стало верным?
 5. Девочка подошла к переходу через улицу в тот момент, когда загорелся жёлтый свет, и загляделась на работу светофора. По своим часам она заметила, что красный свет горит в полтора раза меньше времени, чем зелёный, а жёлтый — в четыре раза меньше, чем красный. После того, как в восемнадцатый раз горел жёлтый свет, зажёгся зелёный, и девочка, простояв 17 минут, стала переходить улицу. Сколько времени горит жёлтый свет?
Задачи второго номера 1982 года
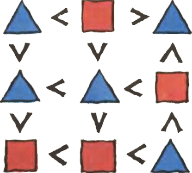 1. В треугольники и квадраты, изображённые на рисунке, впишите первые девять натуральных чисел, причём в треугольники — нечётные числа, а в квадраты — чётные числа так, чтобы все двенадцать соотношений «больше-меньше» были верными.
2. Можно ли из двенадцати одинаковых брусков с квадратными сечениями сделать каркас куба?
 3. При стрельбе по мишени спортсмен несколько раз попал в десятку, столько же раз выбил по 8 очков, и несколько раз попал в пятёрку. Всего он набрал 99 очков. Сколько выстрелов сделал спортсмен?
4. На доске написано несколько ненулевых чисел, каждое из которых равно полусумме остальных. Сколько чисел написано?
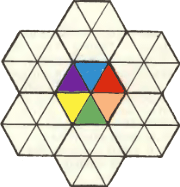 5. Из семи правильных шестиугольников один раскрашен шестью красками. Раскрасьте остальные шестиугольники теми же красками так, чтобы в «цветке», изображённом на рисунке, все треугольные участки, граничащие по сторонам шестиугольников, были окрашены одинаково.
 6. Двигая горизонтальную линейку, положенную ребром на цилиндр, мы перекатываем (без проскальзывания) цилиндр по столу. В начальный момент нулевое деление линейки находилось над точкой касания цилиндра и стола. Где окажется нулевое деление линейки после того, как цилиндр прокатится на 5 см?
Задачи третьего номера 1982 года
 1. В каждом из ребусов ТЭТА + БЭТА = ГАММА и БУКВА · 6 = СЛОВО одинаковым буквам соответствуют одинаковые цифры, разным — разные. (Между собой ребусы никак не связаны.) Расшифруйте эти ребусы.
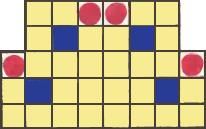 2. Разрежьте изображённую на рисунке фигуру на четыре конгруэнтные части и сложите из них квадрат так, чтобы красные кружочки и синие квадратики оказались симметричными относительно всех осей симметрии квадрата.
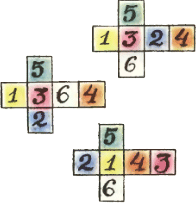 3. Из трёх развёрток, изображённых на рисунке, собрали три кубика; затем из этих кубиков склеили прямоугольный параллелепипед 1×1×3. На четырёх гранях параллелепипеда оказались написаны четыре трёхзначных числа (ориентация цифры в квадрате не имеет значения). Каково наибольшее возможное значение суммы этих чисел?
 4. На столе стоят семь коробочек. Средняя коробочка пустая, а в остальных шести коробочках лежит по две монеты: снизу — пятак, сверху — «двушка». Разрешено перекладывать по одной монете в соседнюю коробочку, но нельзя пятак класть на «двушку». Кроме того, в пятой коробочке не должно оказываться более трёх монет, а в остальных — более двух.
Можно ли переложить монеты так, чтобы а) в первых трёх коробочках лежало по две «двушки», а в последних трёх — по два пятака, б) в первых трёх коробочках лежало по два пятака, а в последних трёх — по две «двушки»?
Задачи четвёртого номера 1982 года
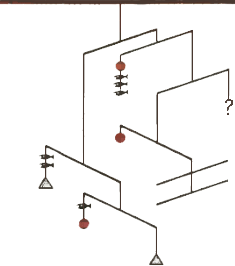 1. Английский популяризатор математики Бернард назвал изображённую на рисунке конструкцию из рыбок, шариков, конусов и палочек «эквилябр», объединив слова «эквилибристика» и «канделябр». Какую массу надо привесить к «свободной палочке» (вопросительный знак на рисунке), чтобы эквилябр находился в равновесии? Найдите массы фигурок, если известно, что масса каждой из палочек равна 10 г.
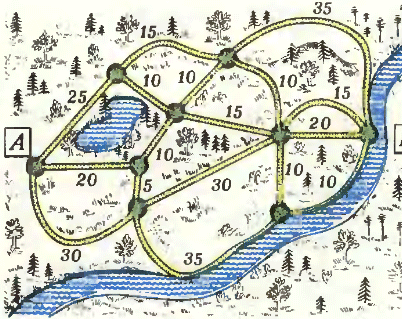 2. Группа туристов хочет попасть из деревни A в деревню B за кратчайшее время (на рисунке рядом с каждой дорогой указано время, которое тратится на её прохождение). Какой маршрут должны избрать туристы?
 3. От основания башни (верхнего красного угла рисунка) за 10 шагов пройдите в нижний красный угол рисунка (шаг — это проход через один участок с числом внутри) так, чтобы сумма чисел пройденных участков равнялась 60.
| |
| Ь | Т | У | Т | У | Т | Ь | Ь | Ь | У | П | Ь
| | У | П | Ь | П | П | Т | У | П | П | П | Т | Т
| | Т | Т | П | Ь | У | Ь | Ь | Ь | Ь | П | П | Т
| | Ь | П | У | П | Т | У | П | Ь | Т | У | Ь | Т
| | П | У | П | П | П | Ь | П | П | П | Т | Т | Т
| | Т | Ь | Т | Т | П | П | Ь | Ь | Т | Ь | П | П
| | Ь | Т | Ь | П | Т | Ь | У | Ь | П | Т | У | Т
| | П | Ь | У | Т | Ь | Т | П | Т | П | Ь | П | У
| | Ь | Т | Ь | Т | П | Т | П | Ь | Т | П | Ь | Т
| | П | Ь | Т | Ь | Т | У | П | П | Т | Т | У | У
| | Т | У | Ь | Т | П | Ь | У | Т | У | Ь | У | Т
| | П | Т | Ь | П | Т | Т | У | Ь | У | У | Т | Ь | |
4. Найдите путь из левой нижней клетки до правой верхней, проходящий через расположенные в квадрате буквы, чтобы он состоял из четвёрок ПУТЬ (именно в такой последовательности).
Задачи пятого номера 1982 года
 1. Можно ли на 24 полях доски размера 8×8 расставить крестики так, чтобы при вычеркивании любых трёх горизонталей и трёх вертикалей оставались невычеркнутыми не менее шести крестиков?
2. Пусть A — натуральное число. Обозначим буквой b число, образованное двумя последними цифрами числа A, буквой a — число, образованное остальными цифрами числа A (например, для A = 2906 получаем a = 29 и b = 6). Докажите, что число A делится на 7 тогда и только тогда, когда а) 2a + b делится на 7; б) 5a – b делится на 7.
3. Существует ли такой год, в котором тринадцатое число ни разу не является понедельником? А какое наибольшее число раз оно может быть понедельником?
4. На каждой из сторон треугольника построено по прямоугольнику. Они соприкасаются вершинами, как показано на рисунке. Докажите, что прямые, соединяющие вершины исходного треугольника с соответствующими вершинами образовавшегося треугольника, пересекаются в одной точке.
5. Можно ли из квадрата размером 5×5 клеток вырезать одну клетку так, чтобы полученную фигуру можно было разрезать по линиям сетки на восемь трёхклеточных прямоугольных полосок?
Задачи шестого номера 1982 года
1. Найдите все такие двузначные числа, состоящие из ненулевых цифр, что если из такого числа вычесть число, полученное перестановкой цифр, то разность окажется квадратом натурального числа. Существует ли такое трёхзначное число, что разность между ним и числом, полученным чтением цифр не слева направо, а справа налево, является квадратом натурального числа?
 2. В ребусах, изображённых на рисунке (по-английски two — это два, six — шесть, twelve — двенадцать), одинаковым буквам соответствуют одинаковые цифры, разным — разные. Звёздочки могут быть любыми цифрами. Расшифруйте эти ребусы.
 3. У Тани и Наташи, взятых вместе, волос на голове на 40 больше, чем у Пети и Васи, а у Тани и Пети — на 20 больше, чем у Наташи и Васи. «Если бы у меня,— подумал Иван Иванович, их сосед,— выросло столько волос, сколько их у Тани, а потом ещё три раза по столько, сколько у Пети, то их у меня стало бы столько, сколько у Васи и трёх Наташ, вместе взятых». Какого цвета волосы у Ивана Ивановича?
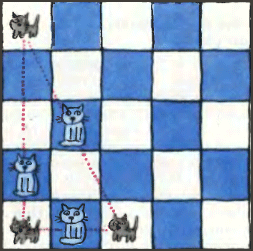 4. В каждой клетке квадрата 5×5 сидит либо котёнок, либо кошка (на рисунке котята — чёрные, а кошки — белые). Если на прямой между двумя котятами находится кошка, то котята не видят друг друга. Какое наибольшее количество котят можно расположить в клетках квадрата так, чтобы ни один котёнок не видел остальных котят?
Задачи седьмого номера 1982 года
 1. На листе бумаги написано число 606. Какое действие нужно совершить, чтобы увеличить его в 1,5 раза?
2. Какой знак нужно поставить между цифрами 5 и 6, чтобы получилось число, большее пяти, но меньшее шести?
3. Часы с боем делают 3 удара за 4 секунды. За сколько секунд они сделают 9 ударов?
4. Сумма чисел 1, 2 и 3 равна их произведению:
Существуют ли ещё такие тройки целых чисел?
5. У меня в кармане две монеты на общую сумму 5 копеек, причём одна из монет не трёхкопеечная. Может ли такое быть? (В 1982 году в ходу были монеты достоинством 1, 2, 3, 5, 10, 15, 20, 50 и 100 копеек.)
6. На рисунке изображена мишень. Можно ли выбить ровно 100 очков? Другими словами, можно ли представить число 100 в виде суммы слагаемых, каждое из которых равно одному из чисел 16, 17, 23, 24, 39, 40?
 7. Останкинская телебашня высотой 530 метров весит 30 000 тонн. Сколько весит точная модель этой башни высотой 53 см?
8. У меня в трёх коробках лежали гвозди, винты и гайки. На каждой коробке было написано, что в ней лежит. Однажды мой младший брат пересыпал содержимое коробок так, что надписи на коробке полностью перестали соответствовать содержимому. Хорошо ещё, что он не перепутал их между собой: гвозди остались лежать отдельно от гаек и винтов, и так далее. Можно ли, открыв только одну коробку, определить, что где лежит?
9. Найдите наименьшее натуральное число, которое после умножения на 2 становится квадратом, а после умножения на 3 — кубом целого числа.
 10. На полке подряд стоят шесть стаканов, как на рисунке: три с водой и три пустых. Как достичь расстановки, при которой пустые и полные стаканы чередуются, если разрешено взять в руку лишь один стакан?
11. Найдите два числа, сумма, произведение и частное которых равны между собой.
 12. На табуретке — коврик, на коврике — стакан с водой. Как убрать коврик, оставив стакан на табуретке, не трогая стакан?
Предлагаем три игры, которые тоже можно использовать в соревнованиях. В каждой из них существует выигрышная стратегия для одного из игроков: начинающего или второго. Определите, кто выигрывает при правильной игре, и найдите выигрышную стратегию.
1. Имеется две кучки камней. Двое играющих делают поочерёдно следующие ходы: забирают одну из кучек, а вторую делят на две части. Если играющий при своем ходе не сможет разделить кучку (так как в ней остался лишь один камень), то он проигрывает.
 2. В землю вбиты несколько колышков. Двое по очереди связывают бечёвками пары колышков. Выигравшим считают игрока, при ходе которого образовалась замкнутая ломаная, составленная из бечёвок. (Не разрешено соединять бечёвкой два ранее уже соединённых колышка.)
3. Двое по очереди обрывают лепестки у ромашки, причём за один раз можно оборвать либо один лепесток, либо два соседних лепестка. Выигрывает тот, кто делает последний ход.
Задачи восьмого номера 1982 года
 1. Костя и Вадик после кино подсчитали оставшиеся у них деньги. Оказалось, что у Кости их в два раза больше, чем у Вадика. Вадик подумал и сказал: «Если бы у нас с тобой было денег в два раза больше, мы купили бы по 4 пряника и выпили по стакану газированной воды по одной копейке за стакан». Более практичный Костя ответил: «Нечего мечтать! Давай купим по 3 конфеты. У нас ещё останется на 3 стакана газировки». Так они и сделали. Сколько денег оставалось у каждого мальчика, если разница в стоимости конфеты и пряника составляет 2 копейки?
 2. Окна в вагонах метро имеют форму, изображённую на рисунке. Закругления верхних углов рамы и стекла обычно делают в виде дуги окружности. Окно приоткрыли, сдвинув стекло на 10 см. Высота подвижной части окна равна 25 см. Чему равна площадь открытой части окна?
 3. В стеклянный сосуд, имеющий форму куба, нужно налить воды на 1/3 его объёма. Как это сделать, не имея никаких измерительных инструментов?
 4. В очереди в школьный буфет стоят Юра, Миша, Володя, Саша и Олег. Юра стоит раньше Миши, но после Олега, Володя и Олег не стоят рядом, а Саша не находится рядом ни с Олегом, ни с Юрой, ни с Володей. В каком порядке стоят ребята?
Задачи девятого номера 1982 года
1. Делимое в 6 раз больше делителя, а делитель в 6 раз больше частного. Чему равны делимое, делитель и частное?
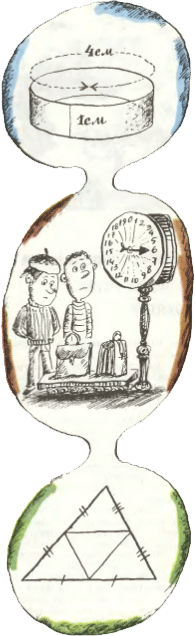 2. Из полоски бумаги шириной 1 см склеили цилиндрическое кольцо с окружностью длиной 4 см, как показано на рисунке. Можно ли из этого кольца изготовить квадрат а) площади 1 квадратный сантиметр; б) площади 2 квадратных сантиметра? Бумагу разрешено как угодно складывать, но рвать её нельзя.
3. Школьники Вадик и Саша увидели весы и взвесили на них свои портфели. Весы показали, что массы портфелей — 3 кг и 2 кг. Когда они поставили на весы оба портфеля, то весы показали 6 кг.
— Как же так?— воскликнул Саша.— Два плюс три не равняется шести!
— Разве ты не видишь? — ответил Вадик.— Просто у весов сдвинута стрелка.
Так сколько же весили портфели на самом деле?
4. Любой треугольник можно средними линиями разрезать на четыре одинаковых треугольника, подобных исходному. Найдите треугольник, который можно разрезать на три одинаковых треугольника, ему подобных.
Задачи десятого номера 1982 года
 1. В детском саду воспитательница кладёт перед ребёнком лист бумаги, на котором нарисовано несколько кружочков.
— Сколько здесь кружочков?— спрашивает она.
— Семь,— отвечает ребёнок.
— Правильно!— говорит воспитательница. Затем она кладёт этот лист перед другим ребёнком и задаёт тот же вопрос.
— Пять,— отвечает ребёнок.
— Правильно!— вновь говорит воспитательница.
Сколько же кружочков нарисовано на бумаге?
2. От чашки с чаем на стену отражается солнечный зайчик. Какой формы тень появится на зайчике, если мы станем сверху приближать к центру поверхности чая чайную ложку?
3. Два пятизначных числа составляют так, чтобы каждая цифра вошла по одному разу в какое-нибудь из этих чисел. Например, 46781 и 50239. Для какой пары таких чисел произведение их будет наименьшим, а для какой — наибольшим?
4. Арбуз разделили тремя разрезами ножа на 7 частей, а когда его съели, то на столе оказалось 8 корок. Второй арбуз разделили четырьмя разрезами ножа на 10 частей. Когда съели его, то на столе от него осталось 12 корок. Третий арбуз разделили четырьмя разрезами ножа на 15 частей. Как разрезали арбузы и сколько корок осталось от последнего?
Задачи одиннадцатого номера 1982 года
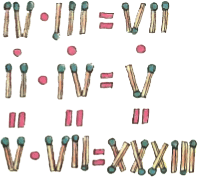 1. В каждом горизонтальном ряду переложите по одной спичке так, чтобы все шесть равенств оказались верными.
 2. На растяжимой верёвке, привязанной к двум противоположным стенкам комнаты, завязаны два узла. Можно ли, не отвязывая и не разрывая верёвки, поменять узлы местами?
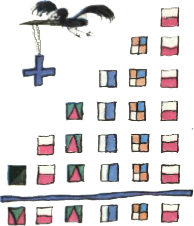 3. Восстановите пример на сложение (разным квадратным фигуркам соответствуют разные цифры, одинаковым — одинаковые).
4. Витя сказал своему другу Коле: «Я придумал пример на деление, в котором делимое, делитель, частное и остаток оканчиваются соответственно на 1, 3, 5 и 7». Подумав, Коля ответил: «Что-то ты путаешь». Прав ли Коля?
Задачи двенадцатого номера 1982 года
 1. Замените звёздочки цифрами в выражении 52*2* так, чтобы полученное число делилось на 36.
 2. На стол кладут одну за другой 8 цветных квадратных салфеток. При этом последующая салфетка закрывает часть хотя бы одной из предыдущих. Определите, какая салфетка была положена первой, и какая из двух салфеток — коричневая или белая — была положена раньше?
 3. Когда секундная стрелка на часах прошла 1 секунду, минутная стрелка прошла 6 минут, хотя часы исправны. Как это объяснить?
4. Для каких двузначных чисел сумма куба числа единиц и квадрата числа десятков равняется самому числу?
5. Какое наибольшее количество чисел можно записать в строку так, чтобы сумма любых 17 последовательных чисел была чётна, а сумма любых 18 последовательных чисел была нечётна?
| 
