«Квант» для «младших» школьников
Задачи первого номера 1981 года
 1. Вырежьте из картона фигуры, изображённые на рисунке. Сложите квадрат, использовав а) каждую из них, кроме квадратика, по одному разу; б) все пять фигур по одному разу; в) каждую из фигур по два раза. 1. Вырежьте из картона фигуры, изображённые на рисунке. Сложите квадрат, использовав а) каждую из них, кроме квадратика, по одному разу; б) все пять фигур по одному разу; в) каждую из фигур по два раза.
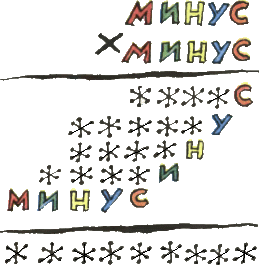 2. Найдите, чему равен МИНУС в примере на умножение, изображённом на рисунке (одинаковым буквам соответствуют одинаковые цифры, разным — разные). 2. Найдите, чему равен МИНУС в примере на умножение, изображённом на рисунке (одинаковым буквам соответствуют одинаковые цифры, разным — разные).
Ответ
Ответ. МИНУС = 14286.
 3. В изображённых на рисунке сорока пяти кружочках, сложенных в треугольник ABC, проставлены цифры от 1 до 9 (каждая цифра повторяется по пять раз, причём никакие две одинаковые цифры не являются соседними). Из вершины A до стороны BC можно добраться 256 различными путями. Но только один из них проходит через все девять цифр. Найдите этот путь. Найдите аналогичные пути из вершин B и C до сторон AC и BC соответственно. 3. В изображённых на рисунке сорока пяти кружочках, сложенных в треугольник ABC, проставлены цифры от 1 до 9 (каждая цифра повторяется по пять раз, причём никакие две одинаковые цифры не являются соседними). Из вершины A до стороны BC можно добраться 256 различными путями. Но только один из них проходит через все девять цифр. Найдите этот путь. Найдите аналогичные пути из вершин B и C до сторон AC и BC соответственно.
Ответ
Ответ. Из вершины А к стороне BC путь проходит по цифрам 1—3—9—6—5—4—2—7—8; из вершины B к стороне AC — по цифрам 7—1—5—3—2—4—6—8—9; из вершины C к стороне AB — по цифрам 2—7—8—9—4—6—5—1—3.
4. Найдите все пятизначные числа с таким свойством: каждая цифра числа строго больше суммы цифр, стоящих правее неё (в частности, четвёртая цифра больше пятой).
Ответ
Ответ. 84 210, 94 210 и 95 210.
5. В Советском Союзе (иначе говоря, СССР) население составляет 260 миллионов человек. Казалось бы, на карте СССР с масштабом 1 : 1 000 000 (в 1 сантиметре — 10 километров) может поместиться в миллион раз меньше людей, чем на всей территории страны, то есть 260 человек. Однако из опыта известно, что это не так. Почему?
Указание
Ответ
Указание. Количество людей, которые могут поместиться на территории, пропорционально не её линейным размерам, а её площади.
Ответ. Масштаб 1 : 1 000 000 означает, что все линейные размеры на карте уменьшены в 106 раз. Поэтому площадь карты, пропорциональная квадрату линейных размеров, меньше площади всей территории СССР в 106 · 106 = 1012 (тысяча миллиардов!) раз.
Задачи второго номера 1981 года
 1. В жаркий летний день представители нескольких фирм собрались на переговоры. Вначале, при обсуждении двусторонних договоров, за каждым столом сидели по два человека — и служители поставили на каждый стол по бутылке минеральной воды. Потом представители разбились на группы по трое — и служители принесли каждой группе по бутылке лимонада. В заключение за каждым столом уселись по четыре человека — и на каждый стол поставили по бутылке фруктового сока. Кроме того, каждый представитель выпил по бутылочке пепси-колы. После совещания со всех столов было собрано 50 пустых бутылок. (Все поданные напитки были выпиты, никто не унёс с собой ни одной бутылки.) Сколько человек участвовало в совещании? 1. В жаркий летний день представители нескольких фирм собрались на переговоры. Вначале, при обсуждении двусторонних договоров, за каждым столом сидели по два человека — и служители поставили на каждый стол по бутылке минеральной воды. Потом представители разбились на группы по трое — и служители принесли каждой группе по бутылке лимонада. В заключение за каждым столом уселись по четыре человека — и на каждый стол поставили по бутылке фруктового сока. Кроме того, каждый представитель выпил по бутылочке пепси-колы. После совещания со всех столов было собрано 50 пустых бутылок. (Все поданные напитки были выпиты, никто не унёс с собой ни одной бутылки.) Сколько человек участвовало в совещании?
Указание
Ответ
Решение
Указание. Искомое количество делится и на 3, и на 4.
Ответ. 24.
Решение. Поскольку искомое количество делится и на 3, и на 4, то оно делится на 12. Проверив числа 12, 24, 36 и 48, получаем ответ: 24.
2. Имеются шестилитровая кастрюля и четырёхлитровая банка. По форме каждая из них — цилиндр. Научитесь наливать из бочки один литр воды.
Указание
Решение
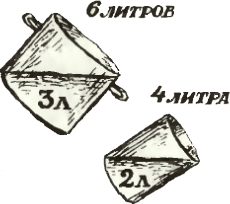 Указание. Указание. В ситуации, изображённой на рисунке, количество воды в каждом из цилиндрических сосудов равно половине его ёмкости.
Решение. Нальём, пользуясь симметрией цилиндра, в кастрюлю 3 литра, а в банку — 2 литра. Перельём теперь воду из кастрюли в банку — в кастрюле останется 1 литр.
 3. Дедушка подарил Пете на день рождения пятирублёвую бумажку. Пошёл Петя в «Спорттовары», чтобы купить компас за 3 рубля. Подошёл к кассе, а кассир говорит: «Чем я тебе сдачу давать буду? У меня одна медь, да и той, боюсь, не хватит!» (В те годы медными называли монеты достоинством 1, 2, 3 и 5 копеек.) Стала набирать 2 рубля: сначала пятаками — пятаки скоро кончились, потом трёхкопеечными монетами — и эти кончились, затем «двушками». Когда кончились и «двушки», набралось 1 рубль 99 копеек, а в кассе осталась одна-единственная копейка. Взяла её кассир и говорит: «Ну, повезло тебе! Ровно 2 рубля набралось!» Взял Петя сдачу, получил компас, собрался уходить и вдруг видит на витрине замечательное увеличительное стекло — и стоит всего-то 1 рубль. Подумал Петя: «Наберётся рубль без сдачи — куплю!» Пришёл он домой и рассказал дедушке всю эту историю. Дедушка подумал секундочку и сказал: «Показывай скорей и компас, и стекло. Посмотрим, такое ли оно замечательное!» Как дедушка догадался, что Петя купил увеличительное стекло? 3. Дедушка подарил Пете на день рождения пятирублёвую бумажку. Пошёл Петя в «Спорттовары», чтобы купить компас за 3 рубля. Подошёл к кассе, а кассир говорит: «Чем я тебе сдачу давать буду? У меня одна медь, да и той, боюсь, не хватит!» (В те годы медными называли монеты достоинством 1, 2, 3 и 5 копеек.) Стала набирать 2 рубля: сначала пятаками — пятаки скоро кончились, потом трёхкопеечными монетами — и эти кончились, затем «двушками». Когда кончились и «двушки», набралось 1 рубль 99 копеек, а в кассе осталась одна-единственная копейка. Взяла её кассир и говорит: «Ну, повезло тебе! Ровно 2 рубля набралось!» Взял Петя сдачу, получил компас, собрался уходить и вдруг видит на витрине замечательное увеличительное стекло — и стоит всего-то 1 рубль. Подумал Петя: «Наберётся рубль без сдачи — куплю!» Пришёл он домой и рассказал дедушке всю эту историю. Дедушка подумал секундочку и сказал: «Показывай скорей и компас, и стекло. Посмотрим, такое ли оно замечательное!» Как дедушка догадался, что Петя купил увеличительное стекло?
Задачи третьего номера 1981 года
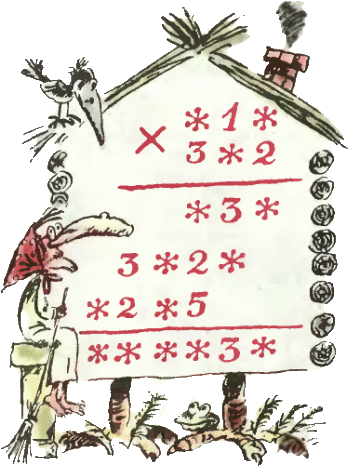 1. В примере, изображённом на рисунке, некоторые цифры заменены звёздочками. Восстановите недостающие цифры. 1. В примере, изображённом на рисунке, некоторые цифры заменены звёздочками. Восстановите недостающие цифры.
2. При каком основании системы счисления число 1111 является полным квадратом? А число 11111?
3. Из девяти цифр 1, 2, 3, ... 8, 9 составьте три трёхзначных числа, которые относятся, как а) 1 : 3 : 5; б) 1 : 2 : 3. Сколько решений имеет задача б)?
4. Сумма цифр трёхзначного числа, все цифры которого различны, кратна 7; само число также делится на 7. Найдите все такие числа.
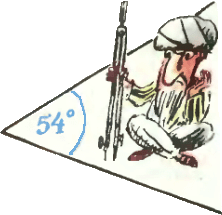 5. Дан угол величиной 54°. Пользуясь только циркулем, разделите его на три равные части (то есть найдите точки так, чтобы лучи, проходящие через вершину данного угла и эти точки, разделили его на три равные части). 5. Дан угол величиной 54°. Пользуясь только циркулем, разделите его на три равные части (то есть найдите точки так, чтобы лучи, проходящие через вершину данного угла и эти точки, разделили его на три равные части).
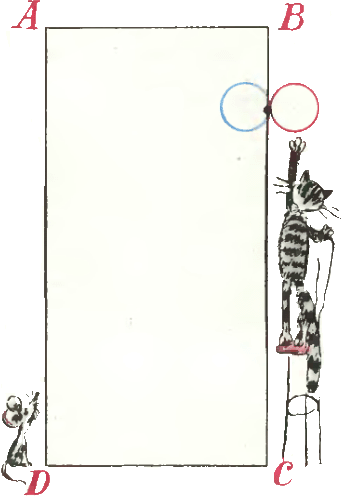 6. Две окружности, длина каждой из которых равна 0,5 м, касаются стороны BC прямоугольника ABCD (|AB| = 1 м, |ВС| = 2 м) в одной и той же точке: одна с внешней стороны, другая — изнутри. Окружности начинают перекатываться по сторонам прямоугольника (находясь в одной с ним плоскости). Сколько оборотов сделает каждая из окружностей к моменту возвращения в исходное положение? 6. Две окружности, длина каждой из которых равна 0,5 м, касаются стороны BC прямоугольника ABCD (|AB| = 1 м, |ВС| = 2 м) в одной и той же точке: одна с внешней стороны, другая — изнутри. Окружности начинают перекатываться по сторонам прямоугольника (находясь в одной с ним плоскости). Сколько оборотов сделает каждая из окружностей к моменту возвращения в исходное положение?
7. По окружности расположены семь монет, лежащих вверх «решкой». Одним ходом разрешено перевернуть любые пять подряд лежащих монет. Можно ли добиться, чтобы все монеты лежали вверх «орлом»?
Задачи четвёртого номера 1981 года
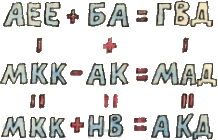 1. В ребусе, изображённом на рисунке, разным буквам соответствуют разные цифры, одинаковым — одинаковые. Расшифруйте peбyc так, чтобы все шесть равенств (например, АЕЕ – МКК = МКК) одновременно стали верными. 1. В ребусе, изображённом на рисунке, разным буквам соответствуют разные цифры, одинаковым — одинаковые. Расшифруйте peбyc так, чтобы все шесть равенств (например, АЕЕ – МКК = МКК) одновременно стали верными.
2. Все числа ряда 0, 4, 18, 48, ?, 180,... получены по некоторой формуле. По какой именно? Какое число пропущено?
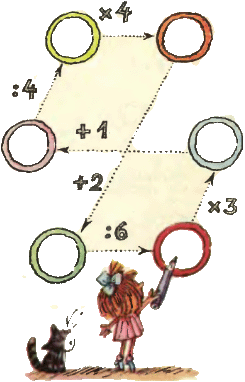 3. Впишите в кружки на рисунке числа так, чтобы каждое следующее в направлении стрелок число получалось из предыдущего при помощи действия, указанного над стрелкой. 3. Впишите в кружки на рисунке числа так, чтобы каждое следующее в направлении стрелок число получалось из предыдущего при помощи действия, указанного над стрелкой.
4. Площадь равнобедренной трапеции, диагонали которой перпендикулярны, равна квадрату её высоты. Докажите это.
5. Десятичная запись натурального числа состоит из 1980 единиц и 1983 двоек, а остальные цифры — нули. Может ли это число быть точным кубом?
 6. В изображённых ниже прямоугольниках сумма чисел в строках одна и та же, суммы чисел в столбцах тоже равны между собой: 6. В изображённых ниже прямоугольниках сумма чисел в строках одна и та же, суммы чисел в столбцах тоже равны между собой:
| 3 | 6 | 6 | 2 | 3 | 2 | 2 | 0
| | 1 | 2 | 4 | 1 | 5 | 2 | 4 | 5
| | 6 | 6 | 1 | 3 | 6 | 2 | 0 | 0
| | 0 | 1 | 4 | 3 | 0 | 5 | 5 | 6
| | 5 | 5 | 0 | 4 | 6 | 2 | 1 | 1
| | 3 | 1 | 2 | 3 | 1 | 4 | 6 | 4
| | 3 | 0 | 4 | 5 | 0 | 4 | 3 | 5 |
| |
| 0 | 1 | 2 | 5 | 1 | 4 | 5 | 6
| | 0 | 1 | 2 | 5 | 1 | 4 | 5 | 6
| | 5 | 2 | 6 | 3 | 3 | 0 | 4 | 1
| | 5 | 2 | 6 | 3 | 4 | 0 | 4 | 1
| | 3 | 4 | 4 | 4 | 2 | 2 | 3 | 3
| | 4 | 6 | 0 | 0 | 6 | 6 | 0 | 2
| | 4 | 6 | 1 | 1 | 5 | 5 | 0 | 2 | |
Сложите сначала один, а затем второй из этих прямоугольников из комплекта домино.
Задачи пятого номера 1981 года
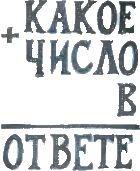 1. Расшифруйте арифметический ребус 1. Расшифруйте арифметический ребус
КАКОЕ + ЧИСЛО + В = ОТВЕТЕ, где разным буквам соответствуют разные цифры, одинаковым — одинаковые, а букве A соответствует чётная цифра.
2. Приведите пример десяти последовательных натуральных чисел, среди которых а) нет ни одного простого числа; б) ровно одно простое число; в) два простых числа; г) три простых числа; д) четыре простых числа.
е) Сколько простых чисел может быть среди десяти последовательных натуральных чисел?
3. На плоскости вокруг точек A и B в одну и ту же сторону поворачиваются два стержня, причём стержень AA' поворачивается вдвое медленнее стержня BB'. В начальный момент угол ABB' прямой, а величина угла BAA' равна 45°. В точке M пересечения этих стержней на них надето колечко. Докажите, что колечко будет двигаться по дуге окружности с центром в точке B. Найдите радиус этой окружности.
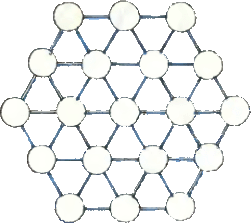 4. В кружках фигуры, изображённой на рисунке, расставьте числа от 1 до 19 так, чтобы сумма чисел, расположенных в кружках-вершинах всех правильных шестиугольников (их девять!), была постоянной. 4. В кружках фигуры, изображённой на рисунке, расставьте числа от 1 до 19 так, чтобы сумма чисел, расположенных в кружках-вершинах всех правильных шестиугольников (их девять!), была постоянной.
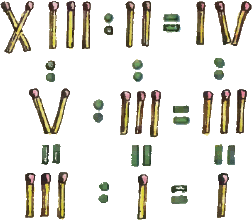 5. В каждом из трёх горизонтальных рядов рисунка переложите по одной спичке так, чтобы все шесть равенств (вертикальных и горизонтальных) оказались верными. 5. В каждом из трёх горизонтальных рядов рисунка переложите по одной спичке так, чтобы все шесть равенств (вертикальных и горизонтальных) оказались верными.
Задачи шестого номера 1981 года
 1. По расписанию поезд из Москвы во Фрунзе отправляется ежедневно в 23 часа 50 минут и находится в пути ровно 75 часов, а поезд из Фрунзе в Москву отправляется ежедневно в 12 часов 50 минут (время московское) и находится в пути (по техническим причинам) 73 часа 28 минут. Состав поезда, прибыв на конечную станцию, отправляется обратно в тот же день. Сколько необходимо сформировать составов, чтобы обеспечить бесперебойную работу маршрута Москва—Фрунзе и обратно? 1. По расписанию поезд из Москвы во Фрунзе отправляется ежедневно в 23 часа 50 минут и находится в пути ровно 75 часов, а поезд из Фрунзе в Москву отправляется ежедневно в 12 часов 50 минут (время московское) и находится в пути (по техническим причинам) 73 часа 28 минут. Состав поезда, прибыв на конечную станцию, отправляется обратно в тот же день. Сколько необходимо сформировать составов, чтобы обеспечить бесперебойную работу маршрута Москва—Фрунзе и обратно?
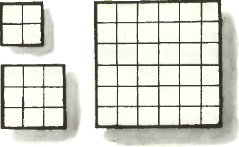 2. Разрежьте квадрат 7×7 на 5 частей, из которых можно (одновременно!) сложить квадраты 6×6, 3×3 и 2×2. 2. Разрежьте квадрат 7×7 на 5 частей, из которых можно (одновременно!) сложить квадраты 6×6, 3×3 и 2×2.
 3. Круглый диск разделен на 21 сектор; секторы одинаковы; в каждый из них записано некоторое число. Во втором диске, укреплённом на одной оси с первым, сделано 5 окошечек так, что при любом повороте второго диска из некоторого начального положения (на угол, кратный одной 21-й части от 360°), в каждое окошечко видно одно из чисел первого диска. Если при любом таком повороте второго диска сумма видных через окошечки чисел равна нулю, то сумма всех чисел, написанных на первом диске, равна нулю. Докажите это. 3. Круглый диск разделен на 21 сектор; секторы одинаковы; в каждый из них записано некоторое число. Во втором диске, укреплённом на одной оси с первым, сделано 5 окошечек так, что при любом повороте второго диска из некоторого начального положения (на угол, кратный одной 21-й части от 360°), в каждое окошечко видно одно из чисел первого диска. Если при любом таком повороте второго диска сумма видных через окошечки чисел равна нулю, то сумма всех чисел, написанных на первом диске, равна нулю. Докажите это.
4. В каждом из ребусов, изображённых на рисунке, одинаковым буквам соответствуют одинаковые цифры, разным — разные. Расшифруйте эти ребусы.
Задачи седьмого номера 1981 года
1. Приходилось ли вам когда-нибудь переставлять буквы в словах, чтобы получались другие осмысленные слова? Например, так: река—каре, серп—перс, мать—тьма, угар—рагу. Подберите парные слова к словам: соха, соль, фазан, весна, салат, плеск, треск, ремонт, нищета, иголка, кордон, вектор, сектор, телескоп, искра, секта, скала, пират, топор, капор (головной убор с завязывающимися под подбородком лентами), сокол, лодка, доска.
Иногда «переставляшки» дают не пару, а тройку, четвёрку, пятёрку или даже шестёрку слов:
марш — ? — ?, спрут — ? — ?, рост — ? — ? — ?, колун — ? — ? — ?, автор — ? — ? — ? — ? — ?.
Какие «переставляшки» вы сумеете придумать ещё?
Ответ
Ответ. Хаос, лось, фанза (одно значение слова фанза — китайский дом с двускатной крышей, преимущественно в сельских местностях, другое — некоторая шёлковая ткань), навес, атлас, склеп, крест, ментор (а вовсе не монтёр), щетина, логика, кондор (птица), корвет (трёхмачтовый корабль), корсет (широкий, упругий пояс для стягивания талии), лепесток, риска, тесак, ласка, тапир, ропот, порка, колос, оклад, садок.
Марш — шрам — шарм (обаяние).
Спрут — спурт (бурный финиш) — струп (сухая корочка на заживающей ране).
Рост — сорт — торс (туловище) — трос.
Колун — клоун — уклон — кулон.
Автор — втора (второй голос в музыкальной партии) — отвар — рвота — товар — тавро.
 2. В клеточки рисунка впишите все десять цифр так, чтобы по горизонталям получились четыре квадрата натуральных чисел. Сколько существует способов это сделать? 2. В клеточки рисунка впишите все десять цифр так, чтобы по горизонталям получились четыре квадрата натуральных чисел. Сколько существует способов это сделать?
Указание
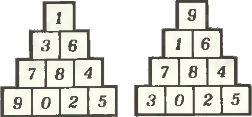 Указание. Указание.
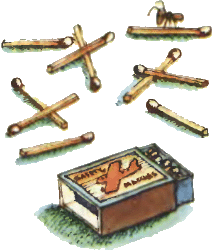 3. Из десяти спичек легко сложить два пятиугольника. А вот сложить из того же количества спичек два пятиугольника и пять треугольников не так-то просто. Попробуйте! 3. Из десяти спичек легко сложить два пятиугольника. А вот сложить из того же количества спичек два пятиугольника и пять треугольников не так-то просто. Попробуйте!
Ответ
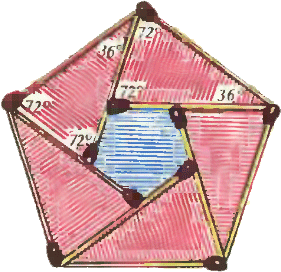 Ответ. Ответ.
4. На листе бумаги расположены 1980 точек, являющихся вершинами правильного 1980-угольника. Два игрока по очереди соединяют эти точки отрезками. За один ход разрешено соединить любые две точки так, чтобы проведённые отрезки не пересекались. Проигрывает тот, у кого нет хода. Кто выигрывает при правильной игре: начинающий или его партнёр?
Указание
Решение
Указание. Воспользуйтесь симметрией.
Решение. При правильной игре выигрывает начинающий: первым ходом он проводит большую диагональ 1980-угольника, а затем соединяет точки, симметричные относительно проведённой диагонали тем, которые только что соединил второй игрок.
Задачи восьмого номера 1981 года
1. При каких значениях n в выражении
* 1 * 2 * ... * n = n + 1
можно так расставить знаки «+» и «–» вместо звёздочек, чтобы получилось верное равенство?
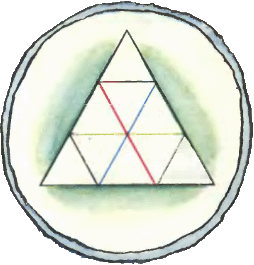 2. Треугольник со стороной 3 разбит на девять маленьких треугольничков со стороной 1, как показано на рисунке. 2. Треугольник со стороной 3 разбит на девять маленьких треугольничков со стороной 1, как показано на рисунке.
а) Расставьте в них числа от 1 до 9 так, чтобы суммы четырёх чисел в трёх треугольниках со стороной 2 были одинаковыми.
б) Какие значения может принимать эта сумма?
 3. Двое детей, запутавшихся в подсчёте дней недели, остановились по дороге в школу, чтобы во всём разобраться. 3. Двое детей, запутавшихся в подсчёте дней недели, остановились по дороге в школу, чтобы во всём разобраться.
— Когда «послезавтра» станет «вчера»,— сказала Присилла,— то «сегодня» будет так же далеко от воскресенья, как и тот день, который был «сегодня», когда «позавчера» было «завтра».
В какой день недели она произнесла этот головоломный лепет?
4. При каких n можно раскрасить клетки квадрата размером n×n в шесть цветов так, чтобы в любом прямоугольнике размером 2×3 (не важно, горизонтально или вертикально расположенном) содержались бы клетки всех шести цветов?
 5. В сказочной стране Перра—Терра среди прочих обитателей проживают карабасы и барабасы. Каждый карабас знаком с шестью карабасами и девятью барабасами. Каждый барабас знаком с десятью карабасами и семью барабасами. Кого в этой стране больше: карабасов или барабасов? 5. В сказочной стране Перра—Терра среди прочих обитателей проживают карабасы и барабасы. Каждый карабас знаком с шестью карабасами и девятью барабасами. Каждый барабас знаком с десятью карабасами и семью барабасами. Кого в этой стране больше: карабасов или барабасов?
Задачи девятого номера 1981 года
 1. В магазин привезли муку в мешках. В первом, втором и третьем мешках не менее 60 кг муки; в первом, втором и четвёртом — не более 50 кг муки; в первом, третьем и четвёртом — не более 40 кг муки; во втором, третьем и четвёртом — не более 30 кг муки. Сколько муки в каждом мешке? 1. В магазин привезли муку в мешках. В первом, втором и третьем мешках не менее 60 кг муки; в первом, втором и четвёртом — не более 50 кг муки; в первом, третьем и четвёртом — не более 40 кг муки; во втором, третьем и четвёртом — не более 30 кг муки. Сколько муки в каждом мешке?
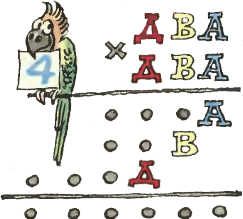 2. Расшифруйте ребус, изображённый на рисунке. Одинаковым буквам соответствуют одинаковые цифры, разным — разные. Точки могут обозначать любые цифры. 2. Расшифруйте ребус, изображённый на рисунке. Одинаковым буквам соответствуют одинаковые цифры, разным — разные. Точки могут обозначать любые цифры.
 3. Однажды придворный Математик, получив свое жалованье за год серебряными талерами, разложил монеты в девять неравных столбиков так, что количества монет в столбиках образовали магический квадрат третьего порядка (то есть квадрат из из девяти чисел, суммы которых по строкам, столбцам и диагоналям одинаковы); при этом некоторые столбики получились довольно высокими, но всё же столбика, который насчитывал бы больше трёхсот монет, не было. Королю понравилась затея Математика; он только пожалел, что все числа получились составными. «Если бы Ваше величество,— сказал Математик,— добавило к моему жалованью ещё 9 талеров, я положил бы в каждый столбик ещё по монете, и тогда сохранился бы магический квадрат, но все количества монет в столбиках были бы простыми». Король совсем уж было собрался увеличить жалованье Математику, как в разговор вмешался Шут. Он взял из каждого столбика по монете, и новые числа все оказались простыми, а квадрат остался магическим! Как сложил свои монеты Математик? 3. Однажды придворный Математик, получив свое жалованье за год серебряными талерами, разложил монеты в девять неравных столбиков так, что количества монет в столбиках образовали магический квадрат третьего порядка (то есть квадрат из из девяти чисел, суммы которых по строкам, столбцам и диагоналям одинаковы); при этом некоторые столбики получились довольно высокими, но всё же столбика, который насчитывал бы больше трёхсот монет, не было. Королю понравилась затея Математика; он только пожалел, что все числа получились составными. «Если бы Ваше величество,— сказал Математик,— добавило к моему жалованью ещё 9 талеров, я положил бы в каждый столбик ещё по монете, и тогда сохранился бы магический квадрат, но все количества монет в столбиках были бы простыми». Король совсем уж было собрался увеличить жалованье Математику, как в разговор вмешался Шут. Он взял из каждого столбика по монете, и новые числа все оказались простыми, а квадрат остался магическим! Как сложил свои монеты Математик?
Задачи десятого номера 1981 года
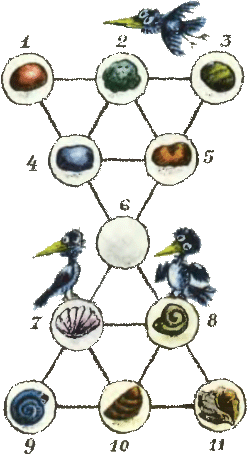 1. На рисунке в кружочках с номерами 1, 2, 3, 4 и 5 лежат камушки (по одному в каждом кружочке); в кружочках с номерами 7, 8, 9, 10, 11 — ракушки (тоже по одной в кружочке). Камушкам и ракушкам разрешено перемещаться вдоль линий на соседний свободный кружочек и перепрыгивать (вдоль линий) через любого соседа на свободный кружочек (вначале свободен кружочек номер 6). Можно ли добиться, чтобы камушки и ракушки поменялись местами? 1. На рисунке в кружочках с номерами 1, 2, 3, 4 и 5 лежат камушки (по одному в каждом кружочке); в кружочках с номерами 7, 8, 9, 10, 11 — ракушки (тоже по одной в кружочке). Камушкам и ракушкам разрешено перемещаться вдоль линий на соседний свободный кружочек и перепрыгивать (вдоль линий) через любого соседа на свободный кружочек (вначале свободен кружочек номер 6). Можно ли добиться, чтобы камушки и ракушки поменялись местами?
 2. Докажите неравенство
ДВА · ШЕСТЬ < ДВАДЦАТЬ, где каждая буква обозначает цифру, причём разным буквам соответствуют разные цифры, одинаковым — одинаковые. 2. Докажите неравенство
ДВА · ШЕСТЬ < ДВАДЦАТЬ, где каждая буква обозначает цифру, причём разным буквам соответствуют разные цифры, одинаковым — одинаковые.
 3. 15 монет расположены в узлах клетчатой бумаги так, как показано на рисунке (в узле номер два монеты нет!). Монета может переместиться в свободный узел, перепрыгнув вдоль линий сетки через свою соседку, которую при этом удаляют. Можно ли, сделав 14 ходов, добиться того, чтобы осталась одна монета? 3. 15 монет расположены в узлах клетчатой бумаги так, как показано на рисунке (в узле номер два монеты нет!). Монета может переместиться в свободный узел, перепрыгнув вдоль линий сетки через свою соседку, которую при этом удаляют. Можно ли, сделав 14 ходов, добиться того, чтобы осталась одна монета?
4. Можно ли все десять цифр расставить по окружности так, чтобы сумма любых трёх из них, идущих подряд, не превышала а) 13; б) 14; в) 15?
5. Существует ли число, произведение цифр которого равно 528?
Задачи одиннадцатого номера 1981 года
1. Клетки квадратной таблицы заполнены единицами, нулями и минус единицами. Могут ли суммы чисел по строкам, столбцам и обеим главным диагоналям все быть разными?
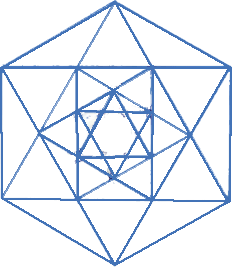 2. Сколько треугольников содержит фигура, изображённая на рисунке? 2. Сколько треугольников содержит фигура, изображённая на рисунке?
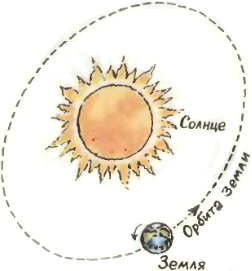 3. Сколько оборотов совершает Земля вокруг своей оси за один год? (Продолжительность года считайте равной 365 дням.) 3. Сколько оборотов совершает Земля вокруг своей оси за один год? (Продолжительность года считайте равной 365 дням.)
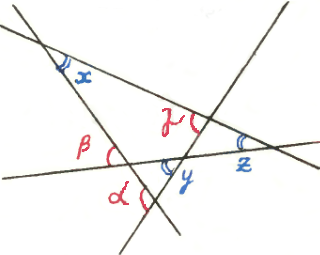 4. На плоскости расположены четыре прямые, как показано на рисунке. Известны величины углов между некоторыми из них: α = 110°, β = 60°, γ = 80°. Найдите величины углов между остальными парами прямых. 4. На плоскости расположены четыре прямые, как показано на рисунке. Известны величины углов между некоторыми из них: α = 110°, β = 60°, γ = 80°. Найдите величины углов между остальными парами прямых.
5. Найдите все двузначные числа, которые делятся на произведение своих цифр.
6. На пакете с фотоплёнкой написано: «Обрабатывать при красном свете». Получится ли на этой пленке пиратский флаг, изображённый на рисунке слева? А флаг, изображённый справа?
 
Задачи двенадцатого номера 1981 года
1. В равенствах a : b = c, c + d = e, e – f = g, g · h = 10i + j замените буквы цифрами так, чтобы получились верные равенства и все цифры от 0 до 9 были использованы.
 2. В изображённом на рисунке коврике, сплетённом из разноцветных верёвок, есть верёвочное кольцо, при разрезании которого коврик распадается на три части так, что две из этих частей состоят из одинакового числа верёвок, а третья — всего из одной верёвки. Укажите это кольцо. 2. В изображённом на рисунке коврике, сплетённом из разноцветных верёвок, есть верёвочное кольцо, при разрезании которого коврик распадается на три части так, что две из этих частей состоят из одинакового числа верёвок, а третья — всего из одной верёвки. Укажите это кольцо.
3. В любом выпуклом семиугольнике есть хотя бы одна пара диагоналей, величина угла между которыми меньше 13°. Докажите это.
4. Толя предложил Ире разрезать прямоугольник размером 8×9 по линиям сетки на прямоугольные полоски 1×6. Сможет ли Ира это сделать?
5. В первой строчке записаны три целых числа: a, b, c. Во второй строчке под ними записаны три разности: a – b, b – c, c – a. Числа каждой следующей строки образованы из чисел очередной строки по этому же закону. Докажите, что ни в одной из строчек ниже седьмой не может встретиться число 279.
| 
