«Квант» для «младших» школьников
Задачи первого номера 1978 года
 1. Из спичек сложили неверное равенство XVI + II = XV. Переложите в этом равенстве одну спичку так, чтобы получить верное равенство. 1. Из спичек сложили неверное равенство XVI + II = XV. Переложите в этом равенстве одну спичку так, чтобы получить верное равенство.
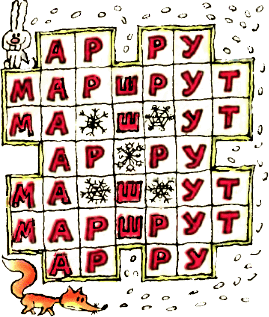 2. Сколькими способами можно прочитать слово МАРШРУТ на орнаменте, изображённом на рисунке, если начинать можно с любой буквы М, а каждую последующую букву выбирать из соседних клеток (соседними считаем клетки, имеющие либо общую сторону, либо общую вершину)? 2. Сколькими способами можно прочитать слово МАРШРУТ на орнаменте, изображённом на рисунке, если начинать можно с любой буквы М, а каждую последующую букву выбирать из соседних клеток (соседними считаем клетки, имеющие либо общую сторону, либо общую вершину)?
 3. В каждом из этих двух ребусов зашифрован процесс сложения столбиком. Одинаковым буквам соответствуют одинаковые цифры, разным — разные. Расшифруйте примеры. 3. В каждом из этих двух ребусов зашифрован процесс сложения столбиком. Одинаковым буквам соответствуют одинаковые цифры, разным — разные. Расшифруйте примеры.
4. Произведение двух двузначных чисел делится на 121 и является четырёхзначным числом, в записи которого участвуют лишь две цифры, причём каждая дважды. Найдите эти числа.
Задачи второго номера 1978 года
1. Найдите два таких двузначных числа БА и ЭТ, что БА · БА = БЭТА, а ЭТ · ЭТ · ЭТ = БЭАТ.
 2. Расшифруйте отрывок из книги «Алиса в Зазеркалье» английского математика и писателя Льюиса Кэррола. Эта книга — продолжение всем известной «Алисы в стране чудес». Отрывок имеет прямое отношение к математике: 2. Расшифруйте отрывок из книги «Алиса в Зазеркалье» английского математика и писателя Льюиса Кэррола. Эта книга — продолжение всем известной «Алисы в стране чудес». Отрывок имеет прямое отношение к математике:
БЕРБИ Э ЙДЕМГОКВЭЫ: БИБЕО-ЖАКЙПЧ ЗВЕЛЕ,— ЗБИСИВ ФИВМИУ-КЕВМИУ ПЕЛЕВЧЖЕ ДГОСГАМОВЧЖЕ,— ЕЖЕ ЕСЖИЬНОМ МЕВЧБЕ МЕ, ЬМЕ Э ЦЕЬЙ, ЬМЕКЮ ЕЖЕ ЕКЕСЖИЬИВЕ,— ЖА КЕВЧФО, ЖА ТОЖЧФО.
Текст зашифрован следующим образом: десять букв — а, е, и, й, о, у, ы, э, ю, я — как-то разбиты на пары, остальные двадцать две буквы (буква «ё» у нас не встречается) тоже как-то разбиты на пары, и каждая буква в тексте заменена на другую из той же пары. Отрывок записан по всем правилам русского языка.
 3. Николай с сыном и Пётр с сыном были на рыбалке. Николай поймал столько же рыб, сколько его сын, а Пётр — втрое больше, чем его сын. Всего было поймано 35 рыб. Сына Николая зовут Григорий. Как зовут сына Петра? 3. Николай с сыном и Пётр с сыном были на рыбалке. Николай поймал столько же рыб, сколько его сын, а Пётр — втрое больше, чем его сын. Всего было поймано 35 рыб. Сына Николая зовут Григорий. Как зовут сына Петра?
4. Какое наибольшее количество месяцев одного года может иметь по 5 пятниц?
Задачи третьего номера 1978 года
 1. Сколько булок было у пекаря? Ответом служит наибольшее возможное число «много» в ребусе БУЛОК + БЫЛО = МНОГО. 1. Сколько булок было у пекаря? Ответом служит наибольшее возможное число «много» в ребусе БУЛОК + БЫЛО = МНОГО.
 2. Средний возраст одиннадцати игроков футбольной команды — 22 года. Во время матча один из игроков получил травму и ушёл с поля. Средний возраст оставшихся на поле игроков стал равен 21 году. Сколько лет футболисту, получившему травму? 2. Средний возраст одиннадцати игроков футбольной команды — 22 года. Во время матча один из игроков получил травму и ушёл с поля. Средний возраст оставшихся на поле игроков стал равен 21 году. Сколько лет футболисту, получившему травму?
 3. Из восьми прямоугольников размером 2×4 и шести прямоугольников размером 2×3 Лёня сложил квадрат размером 10×10. Посмотрев на этот квадрат внимательно, он обнаружил, что в двух случаях стороны этих прямоугольников образуют отрезки, соединяющие противоположные стороны квадрата. Это показалось Лёне некрасивым, и он решил сложить из данных четырнадцати прямоугольников тот же квадрат, но уже так, чтобы подобных отрезков не было. Помогите Лёне, ребята! 3. Из восьми прямоугольников размером 2×4 и шести прямоугольников размером 2×3 Лёня сложил квадрат размером 10×10. Посмотрев на этот квадрат внимательно, он обнаружил, что в двух случаях стороны этих прямоугольников образуют отрезки, соединяющие противоположные стороны квадрата. Это показалось Лёне некрасивым, и он решил сложить из данных четырнадцати прямоугольников тот же квадрат, но уже так, чтобы подобных отрезков не было. Помогите Лёне, ребята!
 4. Возьмите многозначное число, у которого все цифры разные. Возьмите второе число, записанное теми же цифрами (в любом другом порядке). От большего числа отнимите меньшее. Любую отличную от нуля цифру разности обведите в кружочек, а сумму остальных цифр сообщите отгадчику (если разность — число двузначное или однозначное, то назовите оставшуюся цифру или нуль соответственно). Отгадчик угадывает цифру, обведённую в кружочек. Как он это делает? 4. Возьмите многозначное число, у которого все цифры разные. Возьмите второе число, записанное теми же цифрами (в любом другом порядке). От большего числа отнимите меньшее. Любую отличную от нуля цифру разности обведите в кружочек, а сумму остальных цифр сообщите отгадчику (если разность — число двузначное или однозначное, то назовите оставшуюся цифру или нуль соответственно). Отгадчик угадывает цифру, обведённую в кружочек. Как он это делает?
Задачи четвёртого номера 1978 года
 1. Дано трёхзначное число. Найдём сумму его цифр. Затем найдём сумму цифр результата. Каким было исходное число, если его и две полученные суммы можно записать так, как изображено на рисунке (одинаковые фигуры соответствуют одинаковым цифрам, разные — разным)? 1. Дано трёхзначное число. Найдём сумму его цифр. Затем найдём сумму цифр результата. Каким было исходное число, если его и две полученные суммы можно записать так, как изображено на рисунке (одинаковые фигуры соответствуют одинаковым цифрам, разные — разным)?
 2. Имеется несколько кувшинов, среди которых есть два кувшина разной формы, а также два кувшина разного цвета. Докажите, что среди них найдутся два кувшина одновременно и разной формы, и разного цвета. 2. Имеется несколько кувшинов, среди которых есть два кувшина разной формы, а также два кувшина разного цвета. Докажите, что среди них найдутся два кувшина одновременно и разной формы, и разного цвета.
3. Натуральное число a таково, что при делении на a любое нечётное число и его куб дают один и тот же остаток. Найдите все такие числа.
 4. На белую плоскость пролили чёрные чернила. Верно ли, что найдутся удалённые на расстояние 1 метр две точки а) одного цвета; б) разных цветов? 4. На белую плоскость пролили чёрные чернила. Верно ли, что найдутся удалённые на расстояние 1 метр две точки а) одного цвета; б) разных цветов?
Задачи пятого номера 1978 года
 1. Десять человек пришли в гости в галошах. Уходили они по одному, и каждый надевал произвольную пару галош, в которую он мог влезть (то есть не меньшего размера, чем его собственная). Какое наибольшее число людей могло не суметь надеть галоши? 1. Десять человек пришли в гости в галошах. Уходили они по одному, и каждый надевал произвольную пару галош, в которую он мог влезть (то есть не меньшего размера, чем его собственная). Какое наибольшее число людей могло не суметь надеть галоши?
 2. Разрезав фигуру, изображённую на рисунке, на две части, сложите из них квадрат так, чтобы цветные квадратики были симметричны относительно всех осей симметрии квадрата. 2. Разрезав фигуру, изображённую на рисунке, на две части, сложите из них квадрат так, чтобы цветные квадратики были симметричны относительно всех осей симметрии квадрата.
3. У четырёх людей, родившихся в разные годы XX века, суммы цифр возрастов одинаковы, а сумма всех четырёх возрастов — точный куб. Сколько лет старшему из этих людей?
4. Если сумма величин углов ABD и ВСА параллелограмма ABCD равна 90°, то этот параллелограмм — ромб или прямоугольник. Докажите это.
5. Какое трёхзначное число равно кубу числа, записываемого последней цифрой, и одновременно квадрату числа, записываемого второй и первой цифрой?
Задачи шестого номера 1978 года
 1. В соревнованиях по бегу участвовали десять спортсменов: Андрей, Виктор, Ефим, Захар, Иван, Клим, Михаил, Николай, Тимофей и Фёдор (рисунок 1). Спортсмен, первым пришедший к финишу, получил 9 баллов, вторым — 8 баллов, третьим — 7 и так далее вплоть до последнего, который получил 0 баллов. Как распределились баллы, показано на рисунке 2. Определите, сколько баллов получил каждый из десяти спортсменов. Подставьте вместо цифр 67 480, 2 401 240 564, 953 564 начальные буквы имён спортсменов, получивших соответствующее количество баллов. Что у вас получилось? 1. В соревнованиях по бегу участвовали десять спортсменов: Андрей, Виктор, Ефим, Захар, Иван, Клим, Михаил, Николай, Тимофей и Фёдор (рисунок 1). Спортсмен, первым пришедший к финишу, получил 9 баллов, вторым — 8 баллов, третьим — 7 и так далее вплоть до последнего, который получил 0 баллов. Как распределились баллы, показано на рисунке 2. Определите, сколько баллов получил каждый из десяти спортсменов. Подставьте вместо цифр 67 480, 2 401 240 564, 953 564 начальные буквы имён спортсменов, получивших соответствующее количество баллов. Что у вас получилось?
 2. Согните из мягкой проволоки фигуру, при параллельном проецировании которой на различные плоскости получаются буквы С, Л, О, Г, написанные так, как изображено на рисунке. 2. Согните из мягкой проволоки фигуру, при параллельном проецировании которой на различные плоскости получаются буквы С, Л, О, Г, написанные так, как изображено на рисунке.
 3. Две девочки играют в такую игру: по очереди отрывают лепестки у ромашки. За один ход можно оторвать либо один лепесток, либо два соседних (с самого начала) лепестка. Выигрывает девочка, сорвавшая последний лепесток. Докажите, что вторая девочка всегда может выиграть (у ромашки больше двух лепестков). 3. Две девочки играют в такую игру: по очереди отрывают лепестки у ромашки. За один ход можно оторвать либо один лепесток, либо два соседних (с самого начала) лепестка. Выигрывает девочка, сорвавшая последний лепесток. Докажите, что вторая девочка всегда может выиграть (у ромашки больше двух лепестков).
 4. Живут пять братьев: Иван, Степан, Андрей и близнецы Сергей и Агей. Произведение лет Сергея и Агея равно году рождения Андрея, а произведение лет Андрея и Степана равно году рождения Ивана. Как зовут сына Андрея, если он в пять раз моложе своего дяди — тёзки? 4. Живут пять братьев: Иван, Степан, Андрей и близнецы Сергей и Агей. Произведение лет Сергея и Агея равно году рождения Андрея, а произведение лет Андрея и Степана равно году рождения Ивана. Как зовут сына Андрея, если он в пять раз моложе своего дяди — тёзки?
Задачи седьмого номера 1978 года
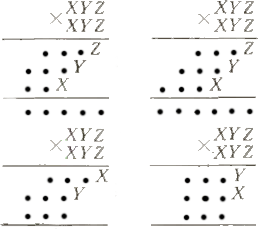 1. Задачи-близнецы. В каждом из четырёх криптарифметических примеров найдите, чему равны значения X и Y. 1. Задачи-близнецы. В каждом из четырёх криптарифметических примеров найдите, чему равны значения X и Y.
 2. На сторонах прямоугольного треугольника площади S как на диаметрах построены полуокружности. Чему равна площадь заштрихованной фигуры? (Для самых маленьких сообщаем теорему Пифагора: сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы: a2 + b2 = c2, где a и b — длины катетов, то есть взаимно перпендикулярных сторон треугольника, c — длина гипотенузы, то есть самой длинной стороны прямоугольного треугольника). 2. На сторонах прямоугольного треугольника площади S как на диаметрах построены полуокружности. Чему равна площадь заштрихованной фигуры? (Для самых маленьких сообщаем теорему Пифагора: сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы: a2 + b2 = c2, где a и b — длины катетов, то есть взаимно перпендикулярных сторон треугольника, c — длина гипотенузы, то есть самой длинной стороны прямоугольного треугольника).
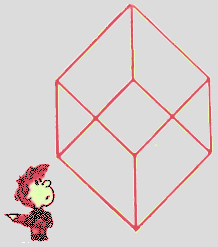 3. Не отрывая карандаша от бумаги, проведите линию, которая пересекла бы по одному разу все 16 отрезков, из которых составлена изображённая на рисунке плоская фигура. 3. Не отрывая карандаша от бумаги, проведите линию, которая пересекла бы по одному разу все 16 отрезков, из которых составлена изображённая на рисунке плоская фигура.
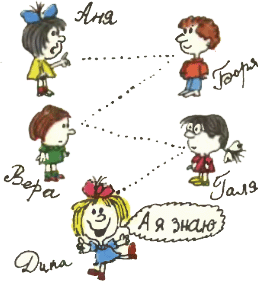 4. Аня задумала натуральное число. Куб этого числа она с остатком разделила на 7. Полученное Аней частное Боря вновь разделил на 7, и тоже — с ненулевым остатком. Новое частное Вера разделила на 7 и не сообщила, получился остаток или нет. Наконец, Галя разделила Верин результат тоже на 7. Частное оказалось равным 10, но был и ненулевой остаток. Дина, узнав все, что проделывалось с Аниным числом, отгадала это число. Какое число задумала Аня? 4. Аня задумала натуральное число. Куб этого числа она с остатком разделила на 7. Полученное Аней частное Боря вновь разделил на 7, и тоже — с ненулевым остатком. Новое частное Вера разделила на 7 и не сообщила, получился остаток или нет. Наконец, Галя разделила Верин результат тоже на 7. Частное оказалось равным 10, но был и ненулевой остаток. Дина, узнав все, что проделывалось с Аниным числом, отгадала это число. Какое число задумала Аня?
Задача восьмого номера 1978 года
 1. Ей было тысяча сто лет, 1. Ей было тысяча сто лет,
Она в сто первый класс ходила,
В портфеле по сто книг носила —
Всё это правда, а не бред.
Когда, пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали.
И десять тёмно-синих глаз
Рассматривали мир привычно...
Но станет всё совсем обычным,
Когда поймёте наш рассказ.
Задачи девятого номера 1978 года
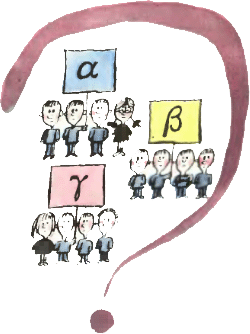 1. В финале школьной математической олимпиады участвовали три команды: «Альфа», «Бета» и «Гамма». Каждая команда должна была составить пять задач и дать их решать своим соперникам. При подведении итогов выяснилось, что команда «Альфа» смогла решить только одну из задач, предложенных командой «Бета», и четыре задачи «Гаммы». Команда «Бета» решила три задачи, предложенные «Гаммой», и две задачи «Альфы». «Гамма» нашла решения всех пяти задач «Альфы», но не смогла решить ни одной задачи «Беты». Общее место присуждалось по итогам двух конкурсов: 1. В финале школьной математической олимпиады участвовали три команды: «Альфа», «Бета» и «Гамма». Каждая команда должна была составить пять задач и дать их решать своим соперникам. При подведении итогов выяснилось, что команда «Альфа» смогла решить только одну из задач, предложенных командой «Бета», и четыре задачи «Гаммы». Команда «Бета» решила три задачи, предложенные «Гаммой», и две задачи «Альфы». «Гамма» нашла решения всех пяти задач «Альфы», но не смогла решить ни одной задачи «Беты». Общее место присуждалось по итогам двух конкурсов:
1) конкурса на сложность (трудность) составленных задач;
2) конкурса на умение решать задачи.
За первое место в каждом конкурсе присуждалось 2 балла, за второе — 1 балл; третье место не оценивалось. Определите, сколько баллов получила каждая команда в обоих конкурсах и каково итоговое распределение мест.
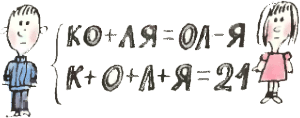 2. Решите изображённую на рисунке систему (буквы К, О, Л, Я нужно заменить цифрами так, чтобы оба равенства сохранились: разные буквы должны соответствовать разным цифрам, одинаковые — одинаковым). Сколько решений имеет система? 2. Решите изображённую на рисунке систему (буквы К, О, Л, Я нужно заменить цифрами так, чтобы оба равенства сохранились: разные буквы должны соответствовать разным цифрам, одинаковые — одинаковым). Сколько решений имеет система?
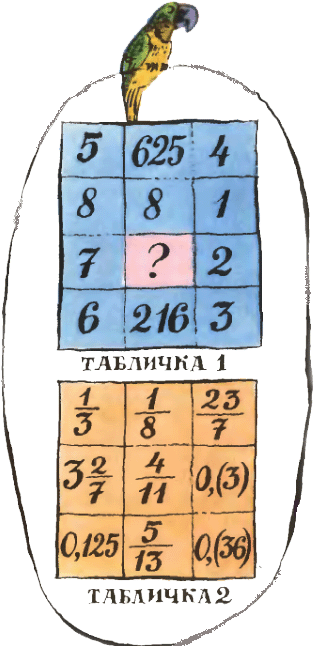 3. Угадав, по какому принципу составлена первая табличка чисел, вставьте недостающее число. Сделав то же со второй табличкой, уберите лишнее число. 3. Угадав, по какому принципу составлена первая табличка чисел, вставьте недостающее число. Сделав то же со второй табличкой, уберите лишнее число.
Задачи десятого номера 1978 года
 1. Сейчас отцу столько лет, сколько месяцев было сыну, когда отец был старше его в 9 раз. Сколько лет сейчас отцу, если известно, что он старше сына на 26 лет 8 месяцев? 1. Сейчас отцу столько лет, сколько месяцев было сыну, когда отец был старше его в 9 раз. Сколько лет сейчас отцу, если известно, что он старше сына на 26 лет 8 месяцев?
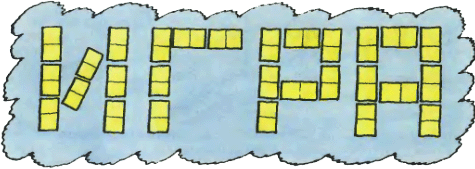 2. Полный комплект косточек домино выложите, как показано на рисунке, чтобы косточки соприкасались по правилам домино, и суммы очков в каждой букве были одинаковыми. 2. Полный комплект косточек домино выложите, как показано на рисунке, чтобы косточки соприкасались по правилам домино, и суммы очков в каждой букве были одинаковыми.
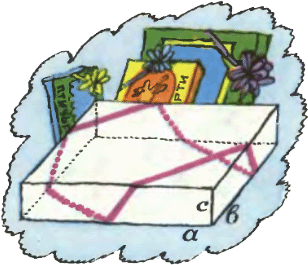 3. Коробка конфет имеет форму прямоугольного параллелепипеда (a — длина, b — ширина, c — высота коробки; коробка — не куб!). Какой длины верёвочки хватит, чтобы перевязать коробку изображённым на рисунке способом? 3. Коробка конфет имеет форму прямоугольного параллелепипеда (a — длина, b — ширина, c — высота коробки; коробка — не куб!). Какой длины верёвочки хватит, чтобы перевязать коробку изображённым на рисунке способом?
 4. В магазин привезли платья трёх разных фасонов и трёх разных расцветок. Продавщица хочет выбрать для витрины три платья так, чтобы были представлены все фасоны и все расцветки. Всегда ли она сможет это сделать? 4. В магазин привезли платья трёх разных фасонов и трёх разных расцветок. Продавщица хочет выбрать для витрины три платья так, чтобы были представлены все фасоны и все расцветки. Всегда ли она сможет это сделать?
Задачи одиннадцатого номера 1978 года
1. а) Если к произвольному числу с нечётным количеством цифр приписать его ещё раз, то полученное число нацело разделится на одиннадцать. Докажите это.
б) Если к произвольному числу приписать число, записанное теми же цифрами, но в обратном порядке, то получим число, кратное одиннадцати. Докажите это.
2. При каких натуральных n число n4 + n2 + 1 является простым?
 3. Семь школьников решили за воскресенье обойти семь кинотеатров. В каждом кинотеатре восемь сеансов; в разных кинотеатрах сеансы начинаются в одно и то же время. На каждый сеанс шестеро школьников шли вместе, а седьмой (не обязательно один и тот же) шёл в другой кинотеатр. К вечеру каждый школьник побывал в каждом кинотеатре. Докажите, что в каждом кинотеатре был сеанс, на котором не присутствовал ни один из этих школьников. 3. Семь школьников решили за воскресенье обойти семь кинотеатров. В каждом кинотеатре восемь сеансов; в разных кинотеатрах сеансы начинаются в одно и то же время. На каждый сеанс шестеро школьников шли вместе, а седьмой (не обязательно один и тот же) шёл в другой кинотеатр. К вечеру каждый школьник побывал в каждом кинотеатре. Докажите, что в каждом кинотеатре был сеанс, на котором не присутствовал ни один из этих школьников.
 4. Беседуя с гостями в конце 1975 года, хозяин пошутил, что многие не любят называть свой возраст: 4. Беседуя с гостями в конце 1975 года, хозяин пошутил, что многие не любят называть свой возраст:
— Я бы, например, на вопрос о возрасте сказал, что мой возраст является делителем моего года рождения.
— Хоть я и значительно моложе,— ответил один из гостей,— но могу то же утверждать и о своём возрасте.
Далее выяснилось, что сын хозяина мог сказать то же о себе в 1961 году, а один из внуков, недавно получивший офицерское звание,— в 1963. А вот покойный отец хозяина мог сказать то же о себе в 1962 году.
В какие же годы родились названные лица?
Задачи двенадцатого номера 1978 года
 1. Внутри прямоугольника в узлах сетки расположены разноцветные точки. Соедините точки одинакового цвета непересекающимися ломаными одинаковой длины так, чтобы звенья ломаных были параллельны сторонам прямоугольника, а длина ломаной была максимально возможной. 1. Внутри прямоугольника в узлах сетки расположены разноцветные точки. Соедините точки одинакового цвета непересекающимися ломаными одинаковой длины так, чтобы звенья ломаных были параллельны сторонам прямоугольника, а длина ломаной была максимально возможной.
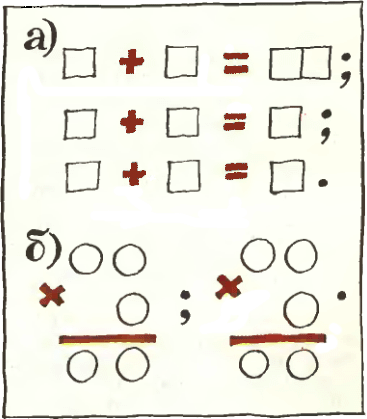 2. а) Впишите в квадратики цифры от 0 до 9 так, чтобы получились три верных примера на сложение. 2. а) Впишите в квадратики цифры от 0 до 9 так, чтобы получились три верных примера на сложение.
б) Впишите в кружочки цифры от 0 до 9 так, чтобы получились два верных примера на умножение.
3. Квадрат составлен из (n + 1)2 квадратных клеточек. Некоторые клетки окрашены в чёрный цвет. Докажите, что всегда можно так закрасить Зn клеток, чтобы при любом вычёркивании n – 1 столбцов и n – 1 строк квадрата оставалась по крайней мере одна белая клеточка.
 4. На пионерском слёте выяснилось, что каждый мальчик знаком ровно с n слетевшимися девочек и каждая девочка знакома ровно с n слетевшимися мальчиками. Докажите, что на слёт слетелось одинаковое количество девочек и мальчиков. 4. На пионерском слёте выяснилось, что каждый мальчик знаком ровно с n слетевшимися девочек и каждая девочка знакома ровно с n слетевшимися мальчиками. Докажите, что на слёт слетелось одинаковое количество девочек и мальчиков.
| 
