«Квант» для «младших» школьников
Задачи первого номера 1976 года
1. В языке племени ододо всего две буквы: «Д» и «О». Два слова означают одно и то же, если одно получается из другого при помощи некоторого количества следующих операций: пропуска идущих подряд буквосочетаний ДО или ООДД и добавления в любое место сочетания ОД. Означают ли слова ОДД и ДОО одно и то же?
 2. Две медные трубки опускают в воду на большую глубину. Одна трубка запаяна с обоих концов, а у другой один конец открыт. Что произойдёт с трубками на глубине? 2. Две медные трубки опускают в воду на большую глубину. Одна трубка запаяна с обоих концов, а у другой один конец открыт. Что произойдёт с трубками на глубине?
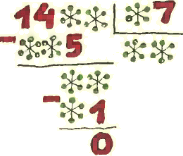 3. Восстановите запись деления, в которой некоторые цифры заменены звёздочками. 3. Восстановите запись деления, в которой некоторые цифры заменены звёздочками.
 4. Известно, что длина тени, которую отбрасывает предмет, в течение дня меняется. Самая короткая тень в полдень, к вечеру тень «растёт». А есть ли на Земле такое место, где длина тени в течение дня не меняется? 4. Известно, что длина тени, которую отбрасывает предмет, в течение дня меняется. Самая короткая тень в полдень, к вечеру тень «растёт». А есть ли на Земле такое место, где длина тени в течение дня не меняется?
5. В игре «Кто первым назовёт число 100» участвуют двое. Один называет любое целое число от 1 до 9 включительно. Второй прибавляет к названному любое целое число от 1 до 9, которое ему понравится, и называет сумму. К этой сумме первый снова добавляет любое целое число от 1 до 9 и называет новую сумму. И так далее. Выигрывает тот, кто первым назовёт число 100. В этой игре начинающий всегда проигрывает, если только его противник откроет один секрет. В чём же секрет, который обеспечивает второму игроку победу?
Задачи второго номера 1976 года
 1. И сказал Кащей Ивану-Царевичу: «Жить тебе до завтрашнего утра. Утром явишься пред мои очи, задумаю три цифры — a, b, c. Назовёшь ты мне три числа — x, у и z. Выслушаю я тебя и скажу, чему равно ax + by + cz. Тогда отгадай, какие a, b, c я задумал. Не отгадаешь — голову с плеч долой». Запечалился Иван-Царевич, пошёл думу думать. Надо бы ему помочь. 1. И сказал Кащей Ивану-Царевичу: «Жить тебе до завтрашнего утра. Утром явишься пред мои очи, задумаю три цифры — a, b, c. Назовёшь ты мне три числа — x, у и z. Выслушаю я тебя и скажу, чему равно ax + by + cz. Тогда отгадай, какие a, b, c я задумал. Не отгадаешь — голову с плеч долой». Запечалился Иван-Царевич, пошёл думу думать. Надо бы ему помочь.
 2. В высокий цилиндрический сосуд диаметром 5 см упал мяч диаметром 4 см. Сможете ли вы достать мяч, не переворачивая сосуд? 2. В высокий цилиндрический сосуд диаметром 5 см упал мяч диаметром 4 см. Сможете ли вы достать мяч, не переворачивая сосуд?
 3. Лаборантка утром взвесила на особо точных весах открытый сосуд с только что вскипевшим маслом. К концу дня, когда масло остыло, она взвесила сосуд ещё раз. Результат взвешивания оказался иным. Почему? 3. Лаборантка утром взвесила на особо точных весах открытый сосуд с только что вскипевшим маслом. К концу дня, когда масло остыло, она взвесила сосуд ещё раз. Результат взвешивания оказался иным. Почему?
 4. Люся переехала в новый восьмиэтажный дом. В нём два подъезда, на каждом этаже четыре квартиры. Когда во дворе ребята спросили Люсю, в какой квартире она живёт, она сказала: «А вы отгадайте. Но на все вопросы я буду только «да» или «нет» отвечать». 4. Люся переехала в новый восьмиэтажный дом. В нём два подъезда, на каждом этаже четыре квартиры. Когда во дворе ребята спросили Люсю, в какой квартире она живёт, она сказала: «А вы отгадайте. Но на все вопросы я буду только «да» или «нет» отвечать».
Один мальчик сказал: «Я буду спрашивать, верно ли, что ты живешь в 1-й квартире, во 2-й, ..., в 63-й? Мне понадобится самое большее шестьдесят три вопроса».
«А мне хватит четырнадцати!— закричал самый маленький. — Этаж я узнаю за семь вопросов, а квартиру — ещё за семь».
А за сколько вопросов вы смогли бы узнать номер Люсиной квартиры?
Задачи третьего номера 1976 года
 1. У нас в классе 35 человек. И можешь себе представить, каждый дружит ровно с 11 одноклассниками... 1. У нас в классе 35 человек. И можешь себе представить, каждый дружит ровно с 11 одноклассниками...
— Не может этого быть,— сразу ответил своему приятелю Витя Иванов, победитель олимпиады.
Почему он так решил?
 2. Виктор пускал в ванне пластмассовый кораблик, нагружённый металлическими деталями от конструктора. Вдруг кораблик наклонился, и детали высыпались в воду. Изменился ли уровень воды в ванне? 2. Виктор пускал в ванне пластмассовый кораблик, нагружённый металлическими деталями от конструктора. Вдруг кораблик наклонился, и детали высыпались в воду. Изменился ли уровень воды в ванне?
 3. В олимпиаде участвовали 55 школьников. Все они сдали свои работы. При проверке каждой задачи ставилась одна из трёх оценок: «+» — задача решена, «–» — задачу решал, но она не решена, «0» — задачу не решал. После проверки всех работ оказалось, что ни в каких двух работах не совпало одновременно количество оценок «+» и оценок «–». Какое наименьшее число задач могло быть предложено на олимпиаде? 3. В олимпиаде участвовали 55 школьников. Все они сдали свои работы. При проверке каждой задачи ставилась одна из трёх оценок: «+» — задача решена, «–» — задачу решал, но она не решена, «0» — задачу не решал. После проверки всех работ оказалось, что ни в каких двух работах не совпало одновременно количество оценок «+» и оценок «–». Какое наименьшее число задач могло быть предложено на олимпиаде?
 4. Выезжая за город на прогулку, хозяйка взяла с собой различные продукты. Так как уксус и подсолнечное масло не смешиваются, она налила обе жидкости в одну бутылку. Можно ли извлечь немного уксуса для салата отцу и немного масла для салата детям так, чтобы остальное масло и остальной уксус остались в бутылке? 4. Выезжая за город на прогулку, хозяйка взяла с собой различные продукты. Так как уксус и подсолнечное масло не смешиваются, она налила обе жидкости в одну бутылку. Можно ли извлечь немного уксуса для салата отцу и немного масла для салата детям так, чтобы остальное масло и остальной уксус остались в бутылке?
Задачи четвёртого номера 1976 года
 1. На шахматной доске на поле f8 стоит ферзь. Двое по очереди передвигают ферзя либо на несколько клеток вниз, либо на несколько клеток влево, либо на несколько клеток влево–вниз по диагонали. Выигрывает тот, кто загонит ферзя в левый нижний угол — на поле a1. Известно, что в этой игре начинающий, если он играет правильно, всегда выигрывает, как бы хорошо ни играл его партнёр. Как же должен играть начинающий, чтобы выиграть? Сколько ходов ему понадобится? 1. На шахматной доске на поле f8 стоит ферзь. Двое по очереди передвигают ферзя либо на несколько клеток вниз, либо на несколько клеток влево, либо на несколько клеток влево–вниз по диагонали. Выигрывает тот, кто загонит ферзя в левый нижний угол — на поле a1. Известно, что в этой игре начинающий, если он играет правильно, всегда выигрывает, как бы хорошо ни играл его партнёр. Как же должен играть начинающий, чтобы выиграть? Сколько ходов ему понадобится?
А кто выигрывает при правильной игре — начинающий или его противник, если вначале ферзь стоит на поле e8?
 2. На дачном участке летом стояла палатка. Когда начались морозы, палатку сняли, а участок решили перекопать. Оказалось, что сухая земля непосредственно под палаткой успела промерзнуть сильнее, чем окружающая более влажная земля. Как это объяснить? 2. На дачном участке летом стояла палатка. Когда начались морозы, палатку сняли, а участок решили перекопать. Оказалось, что сухая земля непосредственно под палаткой успела промерзнуть сильнее, чем окружающая более влажная земля. Как это объяснить?
 3. В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 — в кружке «умелые руки», 10 ребят не ходят в эти кружки. Сколько «математиков» занимаются в «умелых руках»? 3. В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 — в кружке «умелые руки», 10 ребят не ходят в эти кружки. Сколько «математиков» занимаются в «умелых руках»?
 4. Расположите на плоскости одиннадцать одинаковых квадратов, не налегающих друг на друга, так, чтобы выполнялось следующее условие: как бы ни покрасить эти квадраты тремя красками, обязательно какие-нибудь два квадрата одного цвета будут иметь общий участок границы. 4. Расположите на плоскости одиннадцать одинаковых квадратов, не налегающих друг на друга, так, чтобы выполнялось следующее условие: как бы ни покрасить эти квадраты тремя красками, обязательно какие-нибудь два квадрата одного цвета будут иметь общий участок границы.
Задачи пятого номера 1976 года
 1. Три гангстера украли из сейфа 10 бриллиантов общей стоимостью 4 000 000 долларов. При этом они рассчитывали разделить бриллианты так, чтобы каждому досталось не меньше 1 000 000 долларов. При погоне один из бриллиантов стоимостью 600 000 долларов потерялся, и такой раздел стал невозможен. Мог ли он быть возможен вначале, или гангстеры заведомо ошибались? 1. Три гангстера украли из сейфа 10 бриллиантов общей стоимостью 4 000 000 долларов. При этом они рассчитывали разделить бриллианты так, чтобы каждому досталось не меньше 1 000 000 долларов. При погоне один из бриллиантов стоимостью 600 000 долларов потерялся, и такой раздел стал невозможен. Мог ли он быть возможен вначале, или гангстеры заведомо ошибались?
 2. Известно, что вес тела на Луне в 6 раз меньше, чем на Земле. Представьте себе, что вам предложили отправиться на Луну и проверить этот факт экспериментально. Какое оборудование вы возьмёте с собой? 2. Известно, что вес тела на Луне в 6 раз меньше, чем на Земле. Представьте себе, что вам предложили отправиться на Луну и проверить этот факт экспериментально. Какое оборудование вы возьмёте с собой?
 3. Про три точки A, B и C известно, что для любой четвёртой точки M плоскости расстояние от A до M не превосходит хотя бы одного из расстояний BM или CM. Докажите, что точка A лежит на отрезке BC. 3. Про три точки A, B и C известно, что для любой четвёртой точки M плоскости расстояние от A до M не превосходит хотя бы одного из расстояний BM или CM. Докажите, что точка A лежит на отрезке BC.
4. Из двух одинаковых кусков одного и того же металла изготовили две проволоки, одна из которых длиннее другой в 4 раза. Одинаковы или различны сопротивления этих проволок?
5. Имеются 6 одинаковых по виду монет. Четыре из них настоящие, по 4 г каждая, а две фальшивые общим весом 8 г, одна чуть более тяжёлая, другая чуть более лёгкая. Хватит ли четырёх взвешиваний, чтобы с помощью чашечных весов (без гирь) найти обе фальшивые монеты?
Задачи шестого номера 1976 года
 1. В трёх одинаковых коробках лежат по два шарика: в одной — два чёрных, в другой — два белых, в третьей — белый и чёрный. На каждой коробке есть табличка: на одной изображены два белых шарика, на другой — два чёрных, на третьей — белый и чёрный. Содержимое ни одной из коробок не соответствует её табличке. Как, вынув только один шарик только из одной коробки, переставить таблички на коробках в соответствии с их содержимым? 1. В трёх одинаковых коробках лежат по два шарика: в одной — два чёрных, в другой — два белых, в третьей — белый и чёрный. На каждой коробке есть табличка: на одной изображены два белых шарика, на другой — два чёрных, на третьей — белый и чёрный. Содержимое ни одной из коробок не соответствует её табличке. Как, вынув только один шарик только из одной коробки, переставить таблички на коробках в соответствии с их содержимым?
 2. В озере плавает рыба. Она всё время плывёт в горизонтальном направлении. Дно озера очень неровное. Рыба проплывает то над глубокой впадиной, то над подводной горой, то попадает под нависшую скалу. Какие силы действуют на рыбу в этих трёх случаях? 2. В озере плавает рыба. Она всё время плывёт в горизонтальном направлении. Дно озера очень неровное. Рыба проплывает то над глубокой впадиной, то над подводной горой, то попадает под нависшую скалу. Какие силы действуют на рыбу в этих трёх случаях?
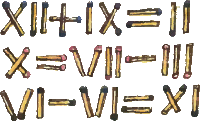 3. Из спичек сложили три неверных равенства: XII + IX = II, X = VII – III и VI – VI = XI. Переложите в каждом равенстве по одной спичке так, чтобы все они стали верными. 3. Из спичек сложили три неверных равенства: XII + IX = II, X = VII – III и VI – VI = XI. Переложите в каждом равенстве по одной спичке так, чтобы все они стали верными.
 4. Два одинаковых прямолинейных магнита соединили один раз так, как показано на верхнем рисунке, другой раз — так, как на нижнем. Нарисуйте линии индукции магнитных полей в этих двух случаях. 4. Два одинаковых прямолинейных магнита соединили один раз так, как показано на верхнем рисунке, другой раз — так, как на нижнем. Нарисуйте линии индукции магнитных полей в этих двух случаях.
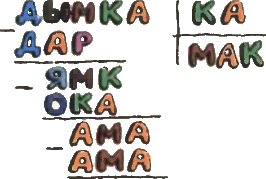 5. На рисунке зашифрован процесс деления (уголком), в котором цифры зашифрованы буквами. Расшифруйте пример. 5. На рисунке зашифрован процесс деления (уголком), в котором цифры зашифрованы буквами. Расшифруйте пример.
Задачи седьмого номера 1976 года
 1. В некотором царстве каждые двое — либо друзья, либо враги. Каждый человек может в любой момент поссориться со всеми друзьями и помириться со всеми врагами. Оказалось, что каждые три человека могут таким образом стать друзьями. Докажите, что тогда и все люди в государстве могут стать друзьями. 1. В некотором царстве каждые двое — либо друзья, либо враги. Каждый человек может в любой момент поссориться со всеми друзьями и помириться со всеми врагами. Оказалось, что каждые три человека могут таким образом стать друзьями. Докажите, что тогда и все люди в государстве могут стать друзьями.
2. Для каких простых чисел p числа 2p + 1 и 4p + 1 тоже простые?
3. Найдите множество центров тяжести треугольников OBA, у которых вершина O фиксирована, а вершины A и B лежат на двух окружностях одинакового радиуса. А что получится, если радиусы окружностей не равны?
 4. Раскрасьте плоскость девятью красками так, чтобы никакие две точки одного цвета не находились на расстоянии 1 метр. 4. Раскрасьте плоскость девятью красками так, чтобы никакие две точки одного цвета не находились на расстоянии 1 метр.
 5. Пароход плывёт из одного города в другой и обратно. Одинаковое ли время затратит пароход, если в одном случае города находятся на берегу реки, а в другом — на таком же расстоянии на берегу озера? Скорость парохода относительно воды постоянна. 5. Пароход плывёт из одного города в другой и обратно. Одинаковое ли время затратит пароход, если в одном случае города находятся на берегу реки, а в другом — на таком же расстоянии на берегу озера? Скорость парохода относительно воды постоянна.
Задачи восьмого номера 1976 года
 1. На рисунке изображён контур колбы, состоящий из дуг равных окружностей. Разрежьте его по двум прямым так, чтобы из полученных частей можно было сложить квадрат. Можно ли сложить аналогичным образом квадрат из второй фигуры? 1. На рисунке изображён контур колбы, состоящий из дуг равных окружностей. Разрежьте его по двум прямым так, чтобы из полученных частей можно было сложить квадрат. Можно ли сложить аналогичным образом квадрат из второй фигуры?
 2. Группа из 21 мальчика получила 200 орехов. Докажите, что как бы ребята ни разделили эти орехи, найдутся двое, которым достанется поровну орехов (может быть, ни одного ореха). 2. Группа из 21 мальчика получила 200 орехов. Докажите, что как бы ребята ни разделили эти орехи, найдутся двое, которым достанется поровну орехов (может быть, ни одного ореха).
 3. В 1815 году английский физик Чилдрен проделал такой опыт. Две платиновые проволочки одинаковых длин, но разных диаметров, он подключал к батарее Вольта. Один раз проволочки были соединены последовательно, а другой — параллельно. В первом случае раскалялась только тонкая проволочка, а во втором — только толстая.
И целых 25 лет не могли ученые объяснить результаты этого эксперимента. А вы можете? Указание: считайте, что количество теплоты, отдаваемое проводником окружающему пространству, пропорционально площади поверхности проводника и разности температур проводника и окружающего пространства. 3. В 1815 году английский физик Чилдрен проделал такой опыт. Две платиновые проволочки одинаковых длин, но разных диаметров, он подключал к батарее Вольта. Один раз проволочки были соединены последовательно, а другой — параллельно. В первом случае раскалялась только тонкая проволочка, а во втором — только толстая.
И целых 25 лет не могли ученые объяснить результаты этого эксперимента. А вы можете? Указание: считайте, что количество теплоты, отдаваемое проводником окружающему пространству, пропорционально площади поверхности проводника и разности температур проводника и окружающего пространства.
4. Найдите все выпуклые многоугольники, обладающие следующим свойством: для любой точки внутренности многоугольника основание перпендикуляра, опущенного из неё на любую сторону, лежит внутри этой стороны.
Задачи девятого номера 1976 года
 1. Группа восьмиклассников решила после окончания учебного года поехать на экскурсию. Ежемесячно каждый ученик вносил одинаковую для всех сумму денег, и за 7 месяцев было собрано 640 рублей 1 копейка. Сколько было в классе учеников? Какую сумму денег вносил каждый ежемесячно? 1. Группа восьмиклассников решила после окончания учебного года поехать на экскурсию. Ежемесячно каждый ученик вносил одинаковую для всех сумму денег, и за 7 месяцев было собрано 640 рублей 1 копейка. Сколько было в классе учеников? Какую сумму денег вносил каждый ежемесячно?
 2. В трёх ящиках лежат орехи. В первом на 6 орехов меньше, чем в двух других вместе, а во втором — на 10 меньше, чем в первом и третьем вместе. Сколько орехов в третьем ящике? 2. В трёх ящиках лежат орехи. В первом на 6 орехов меньше, чем в двух других вместе, а во втором — на 10 меньше, чем в первом и третьем вместе. Сколько орехов в третьем ящике?
 3. «Дайте мне точку опоры, и я переверну мир». Такое заявление сделал Архимед после того, как открыл правило рычага. Поскольку подходящей точки опоры не было (да и сейчас нет), доказать это утверждение экспериментально он не мог. Однако теоретически нетрудно убедиться в том, что Архимед несколько переоценил свои возможности (и возможности рычага). Попробуйте подсчитать, на какое расстояние пришлось бы переместить свободный конец рычага, чтобы приподнять хотя бы на 1 мм тело, масса которого равна массе Земли, то есть приблизительно равна 6 · 1024 кг; среднее усилие, создаваемое рукой человека, примерно 5 ньютон. 3. «Дайте мне точку опоры, и я переверну мир». Такое заявление сделал Архимед после того, как открыл правило рычага. Поскольку подходящей точки опоры не было (да и сейчас нет), доказать это утверждение экспериментально он не мог. Однако теоретически нетрудно убедиться в том, что Архимед несколько переоценил свои возможности (и возможности рычага). Попробуйте подсчитать, на какое расстояние пришлось бы переместить свободный конец рычага, чтобы приподнять хотя бы на 1 мм тело, масса которого равна массе Земли, то есть приблизительно равна 6 · 1024 кг; среднее усилие, создаваемое рукой человека, примерно 5 ньютон.
 4. Из книги выпал её кусок. Первая страница куска имеет номер 387, а номер последней состоит из тех же цифр, но записанных в другом порядке. Сколько страниц выпало из книги? 4. Из книги выпал её кусок. Первая страница куска имеет номер 387, а номер последней состоит из тех же цифр, но записанных в другом порядке. Сколько страниц выпало из книги?
5. Простые числа имеют только два различных делителя — единицу и само это число. А какие числа имеют только три различных делителя?
Задачи десятого номера 1976 года
 1. Мастер спорта Седов, кандидат в мастера Чернов и перворазрядник Рыжов встретились в клубе перед началом турнира. 1. Мастер спорта Седов, кандидат в мастера Чернов и перворазрядник Рыжов встретились в клубе перед началом турнира.
— Обратите внимание,— заметил черноволосый,— один из нас седой, другой рыжий, а третий черноволосый. Но ни у кого цвет волос не соответствует фамилии. Забавно, не правда ли?
— Ты прав,— подтвердил мастер.
Какого цвета волосы у кандидата в мастера?
 2. Золотой призёр школьного чемпионата по футболу набрал 7 очков, серебряный — 5, бронзовый — 3. Сколько очков набрала команда, занявшая последнее место? Сколько команд участвовало в чемпионате? (За выигрыш даётся 2 очка, за ничью — 1, за поражение — 0; если две команды набрали одинаковое количество очков, то места определяются по разности забитых и пропущенных мячей.) 2. Золотой призёр школьного чемпионата по футболу набрал 7 очков, серебряный — 5, бронзовый — 3. Сколько очков набрала команда, занявшая последнее место? Сколько команд участвовало в чемпионате? (За выигрыш даётся 2 очка, за ничью — 1, за поражение — 0; если две команды набрали одинаковое количество очков, то места определяются по разности забитых и пропущенных мячей.)
3. На пяти фишках проставлено по одной цифре: 0, 2, 4, 6, 8. Отберите из этих фишек четыре и расположите их в ряд так, чтобы полученное четырёхзначное число было квадратом некоторого целого числа.
 4. Как вы думаете, будет ли в ракете, в которой все тела находятся в состоянии невесомости, гореть свечка? 4. Как вы думаете, будет ли в ракете, в которой все тела находятся в состоянии невесомости, гореть свечка?
Задачи одиннадцатого номера 1976 года
 1. Поп и Балда играют на «щелбаны» в следующую игру. Они, не показывая друг другу, пишут каждый последовательность из 1976 знаков «плюс» или «минус». После этого выписывают знаки по кругу: первый знак из набора Попа, первый знак из набора Балды, второй знак из набора Попа, второй знак из набора Балды и так далее. Балда даёт Попу столько щелбанов, в скольких местах плюс находится рядом с минусом. Как должен играть Поп, чтобы в наихудшем для себя случае получить поменьше щелбанов? 1. Поп и Балда играют на «щелбаны» в следующую игру. Они, не показывая друг другу, пишут каждый последовательность из 1976 знаков «плюс» или «минус». После этого выписывают знаки по кругу: первый знак из набора Попа, первый знак из набора Балды, второй знак из набора Попа, второй знак из набора Балды и так далее. Балда даёт Попу столько щелбанов, в скольких местах плюс находится рядом с минусом. Как должен играть Поп, чтобы в наихудшем для себя случае получить поменьше щелбанов?
 2. Ученики двух седьмых классов купили 737 учебников. Каждый купил одинаковое количество книг. Сколько было семиклассников и сколько учебников закупил каждый из них? 2. Ученики двух седьмых классов купили 737 учебников. Каждый купил одинаковое количество книг. Сколько было семиклассников и сколько учебников закупил каждый из них?
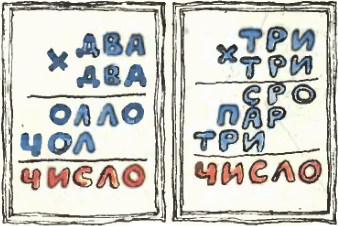 3. На рисунке вы видите два примера на умножение. В каждом примере каждой букве соответствует своя цифра. Какой какая? 3. На рисунке вы видите два примера на умножение. В каждом примере каждой букве соответствует своя цифра. Какой какая?
4. Числа a, b, c, d, e, f, g, h и k отличны от нуля. Докажите, что среди чисел aek, dhc, bfg, –gec, –ahf и –bdk есть хотя бы одно положительное и хотя бы одно отрицательное.
 5. Представьте себе, что в воронку насыпаны мелкие металлические опилки, которые свободно вытекают из «носика» воронки. В опилки воткнута металлическая проволочка, другой конец которой намотан на стеклянную палочку. Что будет происходить с опилками, если палочку натирать куском шерстяной материи? Чтобы убедиться в правильности своего «предсказания», воспроизведите этот несложный опыт. 5. Представьте себе, что в воронку насыпаны мелкие металлические опилки, которые свободно вытекают из «носика» воронки. В опилки воткнута металлическая проволочка, другой конец которой намотан на стеклянную палочку. Что будет происходить с опилками, если палочку натирать куском шерстяной материи? Чтобы убедиться в правильности своего «предсказания», воспроизведите этот несложный опыт.
Задачи двенадцатого номера 1976 года
 1. По случаю избрания Мирафлореса президентом Анчурии был устроен роскошный обед. За круглый стол сели 666 гостей, большинство из которых были лысыми. Назовём двоих сидящих по обе стороны от каждого гостя его соседями; двоих сидящих через одного от него по обе стороны,— его «вторыми соседями» и так далее. Мирафлорес заметил, что для каждого лысого ровно один из его вторых и один из его четвёртых соседей — лысые. Сколько лысых было на обеде? 1. По случаю избрания Мирафлореса президентом Анчурии был устроен роскошный обед. За круглый стол сели 666 гостей, большинство из которых были лысыми. Назовём двоих сидящих по обе стороны от каждого гостя его соседями; двоих сидящих через одного от него по обе стороны,— его «вторыми соседями» и так далее. Мирафлорес заметил, что для каждого лысого ровно один из его вторых и один из его четвёртых соседей — лысые. Сколько лысых было на обеде?
2. В магазине есть на равную сумму конфеты стоимостью 2 рубля за килограмм и конфеты стоимостью 3 рубля за килограмм. По какой цене надо продавать смесь из этих конфет?
3. Из спичек было сложено слово «ТОЛЯ». Переложите одну спичку так, чтобы получилось женское имя.
4. Дана доска 19×19 клеток. На каждой клетке поставлено по шашке. Можно ли переставить шашки так, чтобы каждая шашка оказалась на соседней клетке (по горизонтали или по вертикали, но не по диагонали)?
5. Имеются неправильные весы с двумя чашками и сколько угодно разных правильных гирь. Как отвесить на этих весах один килограмм крупы?
| 
